Evaluating Regression Models

Evaluating Regression Models#

🤔问题回顾：

  • 贝叶斯回归模型和传统的线性回归模型得到的结论是否一致？

贝叶斯回归模型 vs 传统线性回归模型#

首先，让我们回顾上节课定义的三种线性模型，并通过PyMC进行定义和拟合。

模型

参数

解释

model1

RT~Label

简单线性回归模型：自变量为两水平的离散变量

model2

RT~Label+Matching

多元回归模型：自变量为两水平的离散变量和多水平的离散变量

model3

RT ~ Label + Matching + Label:Matching

多元回归模型：自变量额外增加了两个自变量间的交互作用

 
# 导入 pymc 模型包，和 arviz 等分析工具 
import pymc as pm
import arviz as az
import seaborn as sns
import scipy.stats as st
import numpy as np
import matplotlib.pyplot as plt
import xarray as xr
import pandas as pd
import os

# 忽略不必要的警告
import warnings
warnings.filterwarnings("ignore")

try:
  df_raw = pd.read_csv('/home/mw/input/bayes3797/Kolvoort_2020_HBM_Exp1_Clean.csv')
except:
  df_raw = pd.read_csv('/data/Kolvoort_2020_HBM_Exp1_Clean.csv')

df = df_raw.groupby(['Subject','Label', 'Matching'], as_index=False)['RT_sec'].mean()

# 将 Label 列的数字编码转为文字标签
df['Label'] = df['Label'].replace({1: 'Self', 2: 'Friend', 3: 'Stranger'})

df['Matching'] = df['Matching'].replace({'Matching': 'matching', 'Nonmatching': 'nonmatching'})

# 设置索引
df["index"] = range(len(df))
df = df.set_index("index")

# 将 Label 列转换为有序的分类变量
df['Label'] = pd.Categorical(df['Label'], categories=['Self', 'Friend', 'Stranger'], ordered=True)

# 将分类变量转换为哑变量
X1 = (df['Label'] == 'Friend').astype(int)
X2 = (df['Label'] == 'Stranger').astype(int)

# Matching 条件的哑变量
Matching = (df['Matching'] == 'matching').astype(int)  

# Friend 和 Matching 的交互
Interaction_1 = X1 * Matching  

# Stranger 和 Matching 的交互
Interaction_2 = X2 * Matching

# 建立模型1
with pm.Model() as model1:
    # 定义先验分布参数
    beta_0 = pm.Normal('beta_0', mu=5, sigma=2)
    beta_1 = pm.Normal('beta_1', mu=0, sigma=1)
    beta_2 = pm.Normal('beta_2', mu=0, sigma=1)
    sigma = pm.Exponential('sigma', lam=0.3)
    
    # 线性模型表达式
    mu = beta_0 + beta_1 * X1 + beta_2 * X2
    
    # 观测数据的似然函数
    likelihood = pm.Normal('Y_obs', mu=mu, sigma=sigma, observed=df['RT_sec'])

# 建立模型2和模型3

with pm.Model() as model2:
    # 先验分布
    beta_0 = pm.Normal('beta_0', mu=5, sigma=2)  
    beta_1 = pm.Normal('beta_1', mu=0, sigma=1)  
    beta_2 = pm.Normal('beta_2', mu=0, sigma=1)  
    beta_3 = pm.Normal('beta_3', mu=0, sigma=1)  
    sigma = pm.Exponential('sigma', lam=0.3)  
    
    # 线性模型
    mu = beta_0 + beta_1 * X1 + beta_2 * X2 + beta_3 * Matching
    
    # 观测数据的似然函数
    likelihood = pm.Normal('Y_obs', mu=mu, sigma=sigma, observed=df['RT_sec'])

with pm.Model() as model3:
    # 定义先验分布
    beta_0 = pm.Normal('beta_0', mu=5, sigma=2)  
    beta_1 = pm.Normal('beta_1', mu=0, sigma=1) 
    beta_2 = pm.Normal('beta_2', mu=0, sigma=1)  
    beta_3 = pm.Normal('beta_3', mu=0, sigma=1)  
    beta_4 = pm.Normal('beta_4', mu=0, sigma=1) 
    beta_5 = pm.Normal('beta_5', mu=0, sigma=1)  
    sigma = pm.Exponential('sigma', lam=0.3)  
    
    # 线性模型
    mu = (beta_0 + beta_1 * X1 + beta_2 * X2 + beta_3 * Matching +
          beta_4 * Interaction_1 + beta_5 * Interaction_2)
    
    # 观测数据的似然函数
    likelihood = pm.Normal('Y_obs', mu=mu, sigma=sigma, observed=df['RT_sec'])

#===========================
#     注意！！！以下代码可能需要运行3分钟左右
#===========================

def run_model_sampling(save_name, model=None, draws=5000, tune=1000, chains=4, random_seed=84735):
    """
    运行模型采样，并在结果不存在时进行采样，存在时直接加载结果。

    Parameters:
    - save_name: 用于保存或加载结果的文件名（无扩展名）
    - model: pymc 模型
    - draws: 采样次数 (默认5000)
    - tune: 调整采样策略的次数 (默认1000)
    - chains: 链数 (默认4)
    - random_seed: 随机种子 (默认84735)

    Returns:
    - trace: 采样结果
    """
    
    # 检查是否存在保存的.nc文件
    nc_file = f"{save_name}.nc"
    if os.path.exists(nc_file):
        print(f"加载现有的采样结果：{nc_file}")
        # 如果文件存在，则加载采样结果
        trace = az.from_netcdf(nc_file)
    else:

        assert model is not None, "模型未定义，请先定义模型"

        print(f"没有找到现有的采样结果，正在执行采样：{save_name}")
        # 如果文件不存在，则进行采样计算
        with model:
            trace = pm.sample_prior_predictive(draws=draws, random_seed=random_seed)
            idata = pm.sample(draws=draws,                   # 使用mcmc方法进行采样，draws为采样次数
                              tune=tune,                    # tune为调整采样策略的次数
                              chains=chains,                # 链数
                              discard_tuned_samples=True,   # tune的结果将在采样结束后被丢弃
                              idata_kwargs={"log_likelihood": True},
                              random_seed=random_seed)      # 后验采样

            trace.extend(idata)
            # 进行后验预测并扩展推断数据
            pm.sample_posterior_predictive(trace, extend_inferencedata=True, random_seed=random_seed)
            
            # 保存结果到指定文件
        trace.to_netcdf(nc_file)
        
    return trace

# 运行所有三个模型
model1_trace = run_model_sampling("lec10_model1",model1)
model2_trace = run_model_sampling("lec10_model2",model2)
model3_trace = run_model_sampling("lec10_model3",model3)

传统线性回归：

  • 以model3为例，使用statsmodels库中的OLS函数（最小二乘法）来构建一个传统的线性回归模型，并将其结果与贝叶斯模型的结果进行比较：

import statsmodels.api as sm

# 构建设计矩阵
X = sm.add_constant(
    pd.DataFrame({
        'X1': X1, 
        'X2': X2, 
        'Matching': Matching,
        'Interaction_1': Interaction_1,
        'Interaction_2': Interaction_2
    })
)
y = df['RT_sec']

# 传统线性回归模型
model0 = sm.OLS(y, X).fit()

# 打印回归结果
model0.summary()

# 注意，可以通过 az.plot_bf() 函数来计算贝叶斯因子（Bayes Factor）。
az.summary(model3_trace, hdi_prob=0.95)

将两个模型结果进行对比

参数

贝叶斯回归（Bayesian Regression）

传统线性回归（OLS Regression）

\(\beta_0\)

Mean: 0.729, SD: 0.024, HDI: [0.682, 0.775], BF10: 0.2

Mean: 0.7277, SE: 0.024, 95% CI: [0.681, 0.775], \(P=0.000\)

\(\beta_1\)

Mean: 0.047, SD: 0.034, HDI: [-0.021, 0.112], BF10: 0.09

Mean: 0.0488, SE: 0.034, 95% CI: [-0.018, 0.115], \(P=0.149\)

\(\beta_2\)

Mean: 0.032, SD: 0.034, HDI: [-0.034, 0.097], BF10: 0.05

Mean: 0.0326, SE: 0.034, 95% CI: [-0.034, 0.099], \(P=0.333\)

\(\beta_3\)

Mean: -0.051, SD: 0.033, HDI: [-0.117, 0.012], BF10: 0.1

Mean: -0.0501, SE: 0.034, 95% CI: [-0.116, 0.016], \(P=0.139\)

\(\beta_4\)

Mean: 0.032, SD: 0.047, HDI: [-0.061, 0.122], BF10: 0.06

Mean: 0.0305, SE: 0.048, 95% CI: [-0.063, 0.124], \(P=0.523\)

\(\beta_5\)

Mean: 0.058, SD: 0.047, HDI: [-0.034, 0.150], BF10: 0.1

Mean: 0.0568, SE: 0.048, 95% CI: [-0.037, 0.151], \(P=0.234\)

\(\sigma\)

Mean: 0.133, SD: 0.007, HDI: [0.120, 0.147]

-

模型R²

-

R-squared: 0.062

模型调整R²

-

Adjusted R-squared: 0.036

F-statistic

-

F-statistic: 2.362, \(P=0.0418\)

Log-Likelihood

-

Log-Likelihood: 115.01

AIC

-

AIC:-218.0

BIC

-

BIC: -198.7

  • 从结果的对比我们可以看出，贝叶斯回归和传统线性回归在各项参数上都是高度相似的。但是贝叶斯统计有一个好处，那就是可以支持零假设。

模型评估与比较 (Model Evaluation & Comparison)#

在模型评估中，贝叶斯回归和传统线性回归模型在参数估计上的结果非常接近。但是，它们的区别在于对参数的不确定性评估。

  • 贝叶斯模型提供了明确的参数分布，包括 均值、标准差 和 高密度区间（HDI），这使得我们可以更清晰地了解参数估计的不确定性。

  • 而传统线性回归则侧重于给出参数的点估计，并通过 标准误差 和 95% 置信区间 进行评估。虽然传统模型没有明确给出不确定性，但它通过 p 值、R² 等统计量提供了其他重要信息。

🤔思考

传统回归分析提供了更多的 模型评估指标📊，如 R²、调整后的 R²、F 统计量、对数似然、AIC 和 BIC 等。这些指标不仅帮助我们评估模型的拟合优度，还能有效地比较不同模型的复杂性和预测效果。

  • 那么，哪一个模型对于数据的预测效果最好呢？我们又该如何通过这些评估指标来做出更有力的比较呢？

也就是说：

  • 我们需要找到一个最符合我们当前数据特点的模型，这个模型最可能产生我们当前的数据。那么从心理学的角度来讲，它反映的一些变量就能代表我们所关心的、潜在的、无法观测的一些心理过程。

📈💡接下来的步骤：

我们将深入讨论如何使用具体的 评估指标 来量化模型性能，并根据这些指标对模型进行评估和比较。

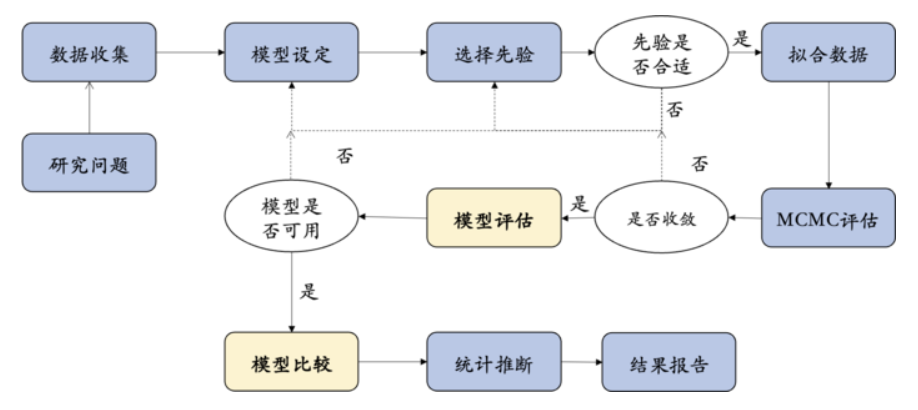
alt text

什么是模型评估？

模型评估则是指对模型是否公平性、有效性、可信性进行评估，既可以是对单个模型，也可以是对多个模型进行。

  • 模型评估与比较(Model evaluation & comparison)的目的在于选择最好的模型。

为什么需要模型比较？

模型

参数

解释

model1

RT~Label

简单线性回归模型：自变量为两水平的离散变量

model2

RT~Label+Matching

多元回归模型：自变量为两水平的离散变量和多水平的离散变量

model3

RT ~ Label + Matching + Label:Matching

多元回归模型：自变量额外增加了两个自变量间的交互作用

1、例如，比较 mode3 和 model2 可以帮助我们确定“Label”和“Matching”之间的交互或调节作用。

2、例如，比较 model2 和 model1 可以衡量增加预测因子是否能提升模型的预测能力。

  • 总之，模型比较的目的随着研究目的的变化而变化。

我们可以从以下三个原则来思考“模型评估与比较”的问题：

1、模型本身公正吗？(How fair is the model?)

  • 公正性(How fair)：模型在数据收集和分析的整个流程中的公正性。

2、模型存在错误吗？(How wrong is the model?)

  • 错误程度(How wrong)：模型在实践中是否有效？即是否能够准确地预测样本数据。

3、后验预测模型有多准确？(How accurate are the posterior predictive models?)

  • 准确性(How accurate)：模型是否反映现实规律？即是否能够准确地预测样本外数据。

模型公正吗？(Is the model fair?)#

模型公正性是一个上位概念，它描述了模型是否符合我们(社会、道德、伦理)的预期，而不仅是关注模型和样本数据的关系。

我们可以借助几个相关问题来理解和思考模型的公正性：

1、数据的收集过程是怎样的？

  • 数据的收集过程直接影响模型的公正性。如果数据收集的过程存在偏见或不充分考虑多样性，那么模型就可能会产生不公正的结果。

  • 例如，某些群体的数据可能被忽视或代表性不足，导致模型结果不具备广泛的适用性或公平性。

2、数据由谁收集，数据收集的目的是什么？

  • 数据收集者的身份、意图和研究目的，都会影响数据的性质和使用方式。

  • 资本主义的核心观念推动了个体主义和竞争性思维，可能导致研究样本的偏倚，削弱了全球不同文化和社会背景的代表性。

我们从实际研究经历出发，可以发现，从数据收集到数据分析的一整个过程中，我们研究者可能会把自身的一些偏见引入其中。例如，最常见的一种数据收集偏见则是采用大学生被试作为样本，但是在大学生群体中得到的结果是否能够推广到整个人口学的大群体可能会存在问题，比如研究结果涉及到政策制定的时候就可能会出现较大偏差，此时考虑群体的多样性问题就变得非常重要。

1. 数据的收集的过程公平吗？

在本示例研究中，数据来源于基于自我匹配范式的实验数据，这些数据通过线下认知实验收集而得。

  • 数据收集过程是公平的，被试填写了实验的知情同意书，并获得相应的报酬。

  • 此外，数据收集过程是匿名化的，保护了被试的隐私。

潜在偏见，如：在数据收集过程中，仅选取大学生群体作为样本，而忽略其他重要的人群。

心理学研究背后的内隐哲学观

在研究过程中未被明确提及，却深刻影响研究设计和解释的潜在观念和假设形成了心理学研究背后的内隐哲学观。

主要包括普遍性假设导致的对文化差异考量不足，以及资本主义核心观念导致的研究样本偏倚。这些内隐观念可能使研究忽视文化多样性和社会不平等，从而影响研究的全面性、准确性和应用价值。

内隐哲学观方面

重要性

作用

影响

新的提倡

普遍性假设与文化差异考量不足

构建准确全面且具文化适应性理论

使研究忽略文化因素，影响各环节

限制理论普适性，阻碍心理学全球发展

数据收集多样化、文化敏感性培训、理论构建多元视角

资本主义核心观念与研究样本偏倚

确保研究样本多样性和代表性

导致样本选择偏向西方或资本主义文化个体

研究结果有偏差，不利于跨文化研究

扩大样本来源、提高研究者文化敏感性、融合多元文化理论

参考文献：Bettache, K. (2024). Where Is Capitalism? Unmasking Its Hidden Role in Psychology. Personality and Social Psychology Review, 0(0). https://doi.org/10.1177/10888683241287570

举例：当我们中国研究者或者非西方研究者在投稿过程中可能会碰到一个问题，那就是当样本全部来自于你所在的地区时，审稿人会认为取样不够国际化，即研究结论不一定能推广到其他种族。然而，当样本是英国或美国群体时，审稿人会觉得没有问题，认为使用英美地区样本得到的研究结果是可以推广到其他种族的，是国际化的。

2. 研究目的，以及数据收集的目的公正吗？

在本示例研究中，研究目的来源自心理学家的好奇和假设。这是合理的，因为心理学研究是一种探索性的研究方法。（无利益冲突）

一些极端的反例：

  • 如果研究项目来源于开发缓解压力药的厂商。那么，研究目的就可能被操纵，以支持药厂的销售。

  • 例如，有目的的选择被试，有目的性的将实验目告诉被试，从而收集到符合预期的数据。

从这张图中，你可以发现什么？🤔

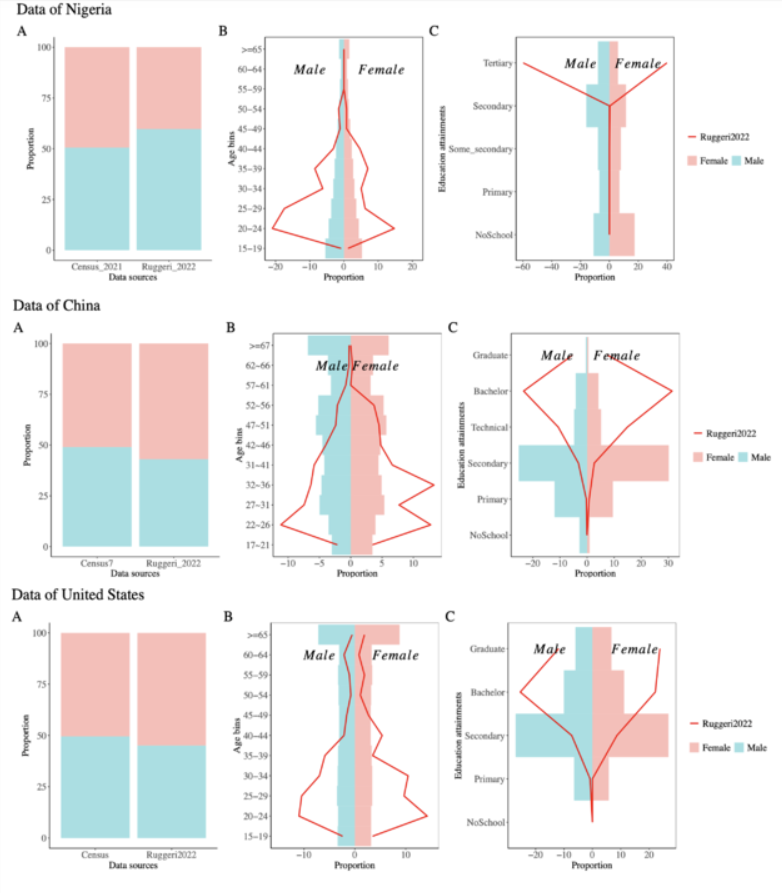
alt text

参考文献：Ghai, S., Forscher, P.S. & Chuan-Peng, H. Big-team science does not guarantee generalizability. Nat Hum Behav 8, 1053–1056 (2024). https://doi.org/10.1038/s41562-024-01902-y

  • 上面是作者自己和其他合作者对一个已发表的数据进行的再分析结果以及可视化。原来的研究认为自己的研究结论可以被叫做globalize，即全世界通用的一个原则。这是因为它在全世界几十个国家收集了数据，因此在数据来源上确实是比较多样化的。

  • 然而，我们来看一些每一个国家的数据，可以看出，无论是尼日利亚、中国还是美国，被试的年龄基本上都集中在18-35之间，也就是说参与研究的绝大部分都是年轻被试。我们再来看被试的受教育程度，这个部分的偏差就更大了，绝大多数参与研究的被试都是受过高等教育的，这实际上和各自国家的实际不符。因此，如果这样的研究结论用以指定某些国际性政策的话，它会涉及很大程度上的偏见。

数据由谁收集，数据收集的目的是什么？

数据收集者的身份、意图和研究目的，都会影响数据的性质和使用方式。

研究者可能内隐地假设心理学现象具有普遍性，但未充分考虑文化差异，这种内隐假设影响了结果的解释，忽视了不同社会和文化背景对心理现象的深刻影响(Ghai, Forscher, & Chuan-Peng, 2024)。

3.模型分析的结果，将对个人和社会产生什么影响？

在本示例研究中，研究结果(模型分析的结果)具有一定的理论意义和实际意义。

  • 在理论层面， 自我匹配范式中的模型能够帮助揭示个体如何处理与“自我”相关的信息。

  • 在实际意义层面，通过这些模型，可以更精确地识别个体在自我认知过程中的偏差。

4. 分析过程中包含的偏见？

一些反例：

  • 假设在一次研究中使用多种问卷收集多种因变量，然后选择有相关性的变量进行报告?

  • 在多因素实验设计中，通过增加变量来获得显著的交互作用，并尝试多种简单效应分析。

在心理学研究中，模型公正性往往与”心理学研究的可重复性”相关。

  • 数据的收集过程是怎样的？

  • 数据由谁收集，数据收集的目的是什么？

  • 数据收集的过程，以及分析的结果，将对个人和社会产生什么影响？

  • 分析过程中可能会包含哪些偏见

  • p-hacking/HARKing

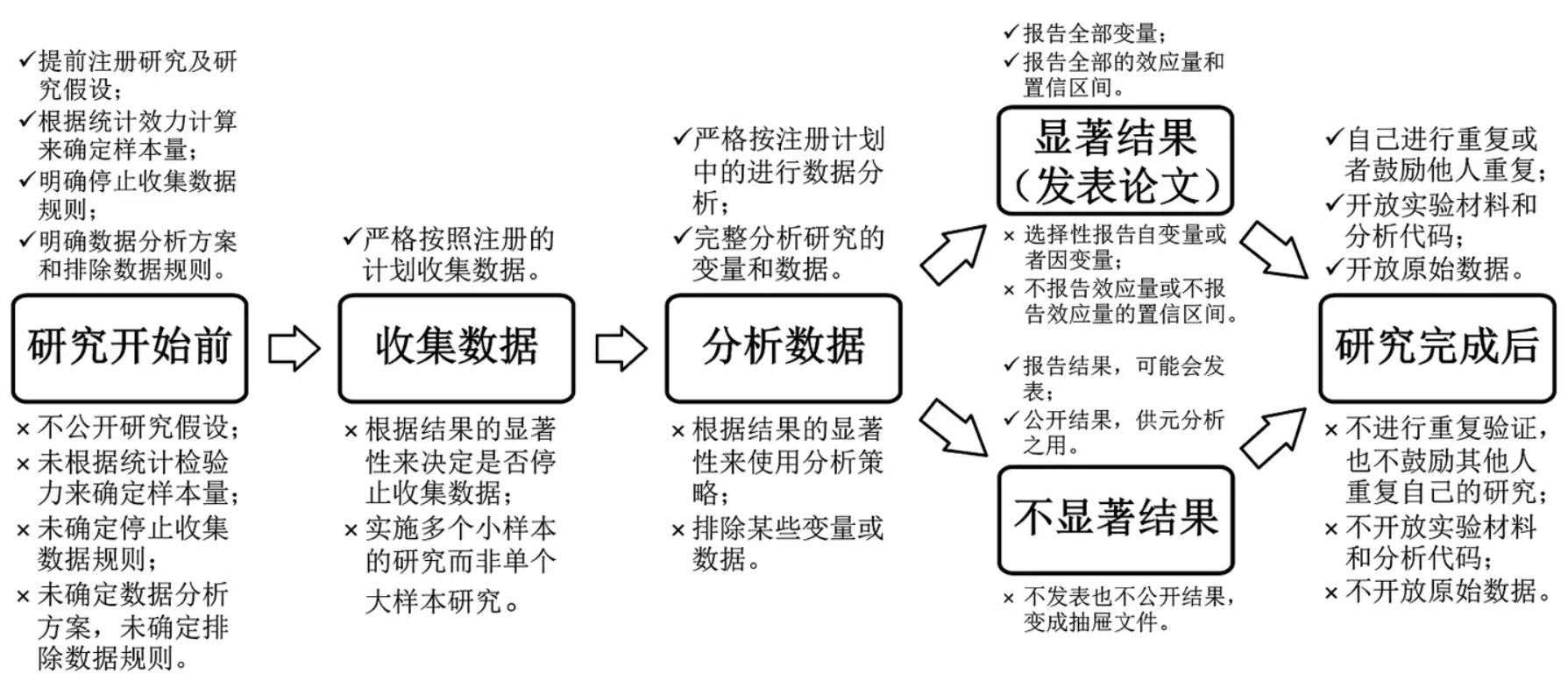
alt text

来源：胡传鹏, …, 彭凯平. (2016). 心理学研究中的可重复性问题:从危机到契机. 心理科学进展, 24(9), 1504-1518. doi: 10.3724/SP.J.1042.2016.01504

这个模型可能有多错误(How wrong is the model?)#

\[ “all~models~are~wrong, but~some~are~useful. ——~George Box” \]

我们一般讲模型的时候都会引用George Box的话——“所有模型都是错误的，但有一些模型是有用的。”

🤔为什么会这么说呢？

实际上，我们在评估模型或比较模型时，并不是说哪个模型一定是对的，因为我们都知道没有绝对正确的模型。因此，我们关注的是模型错误的程度怎么样，以及模型多大程度上与现实相符合。

  • 尽管统计模型是对更复杂现实的简化表达，良好的统计模型仍然可以是有用的，并可以增进我们对世界复杂性的理解。

  • 因此，在评估模型时，要问的下一个问题不是模型是否错误(is the model wrong?)，而是模型错误的程度(How wrong is the model?)

🤔思考贝叶斯线性回归模型的假设在多大程度上与现实相符？

模型假设的影响#

🤔 我们知道模型存在前提预设(assumption)，如果这些模型的前提预设不成立，模型会变得多糟糕？

在lec9中，我们使用一个线性模型来定义标签“Label”与反应时间“RT”之间的关系，并且指定了该模型成立的一些前提预设。

\[\begin{split} Y_i=\beta_0 + \beta_1X_i + \epsilon ~~~ \epsilon\sim N(0,\sigma^2) \\ Y_i|\beta_0,\beta_1,\sigma \overset{ind}{\sim} N(\mu_i,\sigma^2)~with~\mu_i=\beta_0+\beta_1X_i \end{split}\]

回归模型需要满足如下假设：

1.独立观测假设：每个观测值\(Y_i\)是相互独立的，即一个观测值不受其他观测的影响

2.线性关系假设：预测值\(\mu_i\)和自变量\(X_i\)之间可以用线性关系来描述，即：\(\mu_i=\beta_0+\beta_1X_i\)

3.方差同质性假设：在任意自变量的取值下，观测值\(Y_i\)都会以\(\mu_i\)为中心，同样的标准差\(\sigma\)呈正态分布变化。

当假设1 (独立观测假设) 被违反时：

  • 在心理学的实验数据中，观测值之间常常存在依赖关系 (dependent)。

  • 比如，反应时数据在单个被试内、或某种特定刺激类型内可能表现得更加同质：

（1）有的被试（Participant）总是比其他人反应得更快；

（2）有的刺激类型（Stimulus）可能总是导致更快的反应。

这种观测值的相互关联会导致对结果的不准确估计，具体体现在：

  • 过低的标准误：错误高估了参数的显著性；

  • 错误的效应估计：未能正确捕捉组间差异。

解决这种关联问题需要采用层级模型（Hierarchical Models），特别是层级贝叶斯模型（Hierarchical Bayesian Models）。这种方法能够同时建模个体差异（如被试间的反应）和组间差异（如刺激类型的影响）。

例如，在下图中：

  • 左图可能低估了被试间的变异性，假设所有被试的反应时间都完全由刺激难度解释。

  • 右图通过引入随机截距（Random Intercept）更好地捕捉了被试间的差异，使得模型更贴合数据的实际结构。

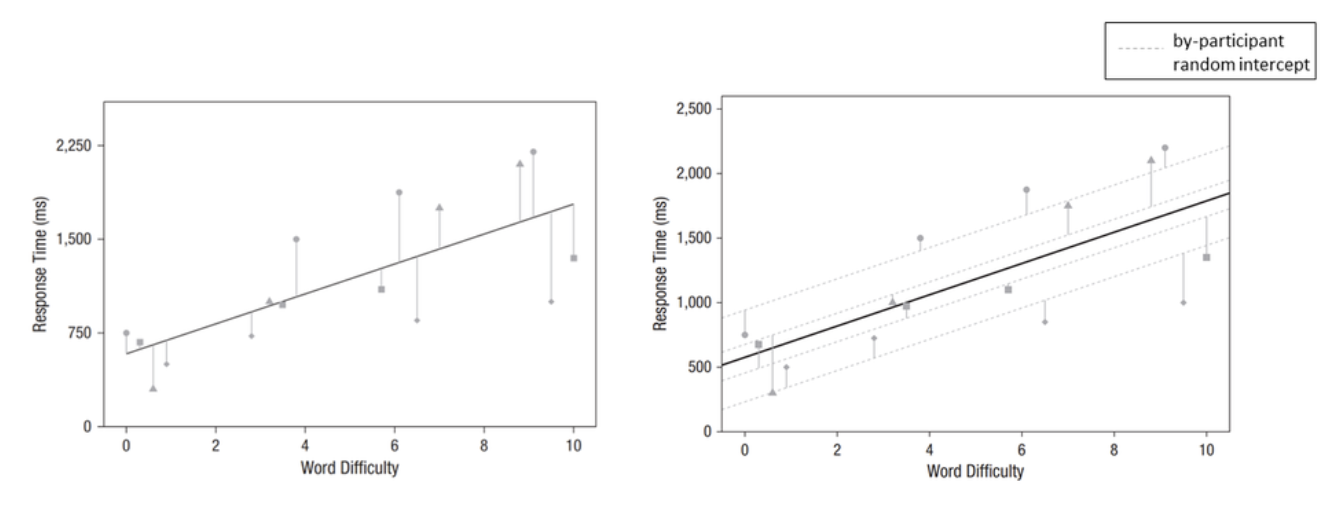
alt text

1、左图：单一模型（无随机效应）

  • 仅考虑整体平均效应，没有控制“被试”或“刺激”的特定差异。

  • 每个数据点的误差条（灰色线条）表示高水平的变异性，线性趋势可能无法很好地反映个体间差异。

2、右图：考虑随机截距模型（Random Intercept Model）

  • 模型中引入了被试间的随机截距（by-participant random intercept），将不同被试的反应时间（RT）的基本差异纳入建模过程。

  • 虚线代表各被试的随机截距，展示了“被试间”的系统性差异；实线代表整体效应估计（包含群体水平的趋势）。

  • 结果更加细化，并能够同时反映群体趋势和个体变异。

source: Brown, V. A. (2021). An Introduction to Linear Mixed-Effects Modeling in R. Advances in Methods and Practices in Psychological Science, 4(1), 2515245920960351. https://doi.org/10.1177/2515245920960351

当假设2(线性关系假设)和假设3(方差同质性假设)被违反时：

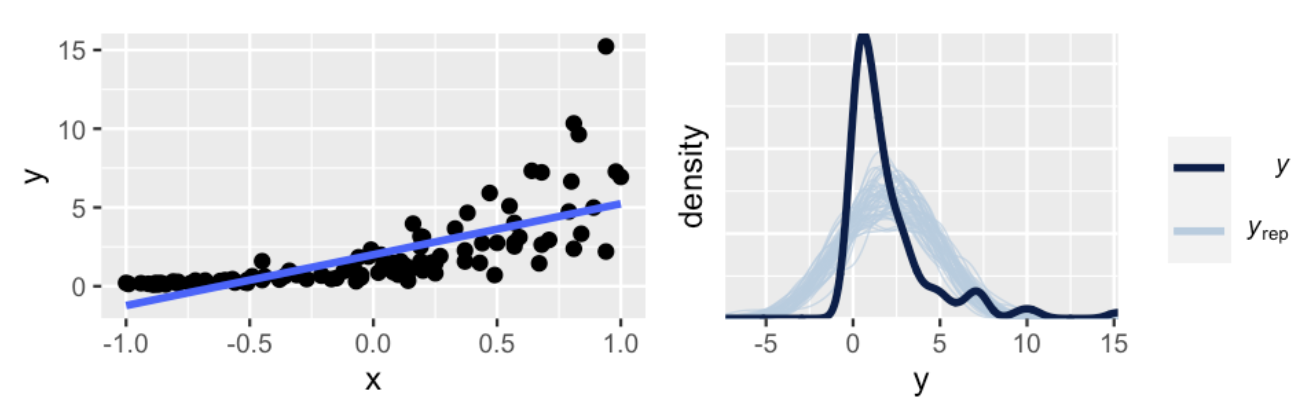
  • 假设2(线性关系假设)违反的情况：在左图中，我们可以看到，Y和X之间的关系并非线性的，更像是一种曲线关系。

假设3(方差同质性假设)违反的情况：并且，随着X的增大，Y的变异性越来越大。

这要导致的后果是，后验预测分布比实际观测值的分布差异很大(右图)

alt text

对模型进行修改

  • 考虑到并不是所有数据都会满足这些假设，当这些假设被违反时，我们需要考虑修改模型。

  1. 对于违反假设1 的情况，我们在之后会学习使用层级贝叶斯模型来处理相互关联的数据。

  2. 对于违反假设2和3的情况，通常有两种处理方式

a. 使用不同的数据模型

不假设实际值与观测值之间的关系是正态的\(Y_i \sim N(\mu_i,\sigma^2)\)

我们后续会学习使用其他回归模型来描述其数据关系，比如泊松回归、二项回归、负二项回归。

b. 对数据进行变换

如果数据模型并不是我们要担心的问题，我们可以对数据进行变换，仍然可以对变换后的数据可以使用正态模型：

  • 对Y进行变换：\(g(Y_i)|\beta_0,\beta_1,\sigma \overset{ind}{\sim}N(\mu_i,\sigma^2),\mu_i=\beta_0+\beta_1X_i\)

  • 对X进行变换：\(Y_i|\beta_0,\beta_1,\sigma \overset{ind}{\sim}N(\mu_i,\sigma^2),\mu_i=\beta_0+\beta_1h(X_i)\)

  • 同时对Y和X进行变换：\(g(Y_i)|\beta_0,\beta_1,\sigma \overset{ind}{\sim}N(\mu_i,\sigma^2),\mu_i=\beta_0+\beta_1h(X_i)\)

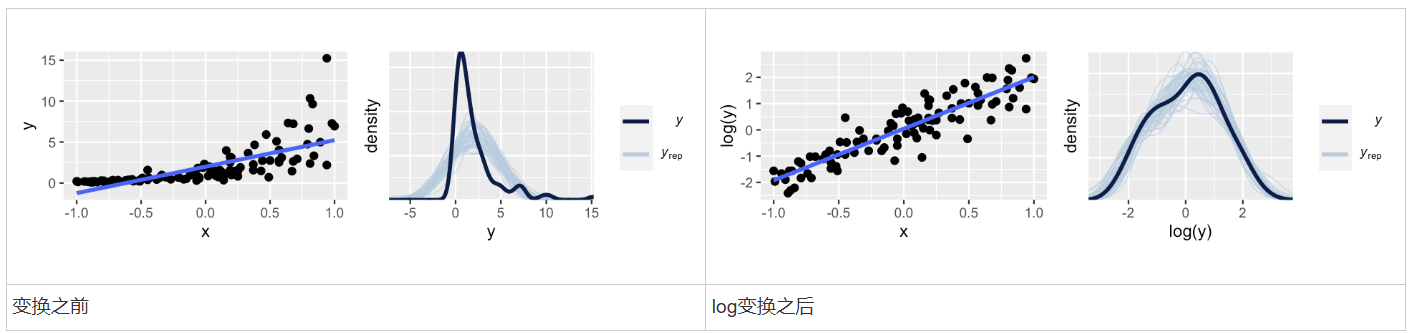
在刚才的例子中，我们对Y的取值进行了一个对数变换

\[ log(Y_i)|\beta_0,\beta_1,\sigma \overset{ind}{\sim}N(\mu_i,\sigma^2)~with~\mu_i=\beta_0+\beta_1X_i \]

  • 在变换之后，可以看到log(Y)与X之间的关系仍然是线性的，且随着X的增大，Y的变异性仍然是一致的。

  • 可以使用正态的线性模型来拟合log(Y)的后验分布。

  • 这部分内容将在逻辑回归（logistics regression）部分进行详细介绍，这里先不作深入解释。

alt text

模型评估#

一般情况下，我们的贝叶斯模型不会是完全不公平的，或者错得太离谱的。 但除了这些问题，更为重要的是，模型是否可以用来准确预测新数据 Y 的结果。

  • 如果说模型公平性和模型错误描述的是模型在质量上的优劣，那模型评估与比较就是在数量上衡量模型预测的准确性。

我们可以通过什么指标来评估预测模型的整体质量呢？

  • 绝对指标，衡量模型对于样本的预测能力。

  • 相对指标，衡量模型对于样本外数据的预测能力，也考虑了模型的复杂度。

首先，先向大家介绍可用于评估模型在样本数据上的预测能力的绝对指标 —- 绝对误差的中位数，median absolute error (MAE)

  • 用以衡量观测值与其后验预测均值之间的典型差异。

绝对误差的中位数，median absolute error (MAE)#

定义：MAE是观测值（\(Y_i\)）和后验预测均值（\(Y_i'\)）的绝对误差的中位数，公式为：

\[ MAE = median(|Y_i-Y_i'|) \]

  • \(Y_i\):实际观测值

  • \(Y_i'\)：模型后验预测的均值

  • 假设\(Y_1,Y_2......,Y_n\)表示n个观测结果

  • 每个\(Y_i\)都有对应的后验预测值，其均值为\(Y_i'\)

作用：衡量模型预测值和实际观测值之间的典型差异。

特点：

  • MAE是绝对误差的典型值，对异常值的敏感性较低。

  • 作为绝对指标，直接反映模型的预测精度。

相对指标：样本外预测能力

仅在样本数据上评估模型并不足以验证其泛化能力，尤其是心理学数据经常受到时间和抽样偏差的影响。例如：

  • 比如，个体的压力状态可能随着季节变化，因此在不同季节收集到的数据会受到时间的影响。

  • 抽样差异：训练模型的数据可能来自理工科学生，而测试模型的数据来自心理学学生，这种抽样差异可能导致预测性能下降。

  • 因此，一种更高效的方法是，一次性多收集一些数据，选择其中的一部分作为预测数据。

相对指标更多的是评估模型在样本外数据上的，同时考虑模型的复杂度,这更有利于比较不同模型的预测能力。

交叉验证(cross validation)#

但问题在于，我们选择哪一部分数据作为预测数据？或者说，我们该如何有效的对数据进行抽取？

交叉验证(cross validation) 的目的就在于：提供不同的抽取预测数据的策略。

其关键在于从已有样本中拿出一部分数据当作预测数据。

alt text

source:【绝对干货】机器学习模型训练全流程！- 知乎 https://zhuanlan.zhihu.com/p/184673895

常见的交叉验证策略：

  1. 分半交叉验证 (Split-half cross-validation)

分半交叉验证将观测数据对半分成两部分，分别在不同的数据集上拟合模型，并在另外一半数据集上验证模型，最后再对比不同的模型在两份数据集作为验证集时的预测准确度。

  1. K 折交叉验证 (K-fold cross-validation)

K 折交叉验证把数据分成 K 份，其中一份作为训练集（拟合模型，对参数进行估计），其余的 K-1 分数据集作为验证集，总共重复这个流程 K 次。以 K 次验证结果的均值作为验证标准。

  1. 留一法交叉验证 (Leave-one-out cross-validation)

留一法交叉验证是 K 折交叉验证的一个特例，当分折的数量等于数据的数量时，K 折留一法便成了留一法交叉验证。留一法交叉验证相较于普通的交叉验证方法，几乎使用了所有数据去训练模型，因此留一法交叉验证的训练模型时的偏差 (bias) 更小、更鲁棒，但是又因为验证集只有一个数据点，验证模型的时候留一法交叉验证的方差 (Variance) 也会更大。

K 折交叉验证 (K-fold cross-validation)

K 折交叉验证在分半交叉验证的基础上，将数据集分成 K 份(称为 CV-K)，其中一份作为测试集，其余 K-1 份作为训练集，重复这个流程 K 次。

K 折交叉验证，以 K 次测试结果的均值作为验证标准。例如，在压力-自我控制的例子中：

  • 我们可以使用 K=5 折的交叉验证，将数据集分成 5 份，每次使用 4 份数据作为训练集，1份数据作为测试集。

  • 对每一次迭代，我们使用 4 份数据训练模型，然后使用剩下的一份数据进行测试，并计算相应的MAE。

  • 重复这个流程 5 次，然后取每次MAE测试结果的均值作为最终的测试结果。

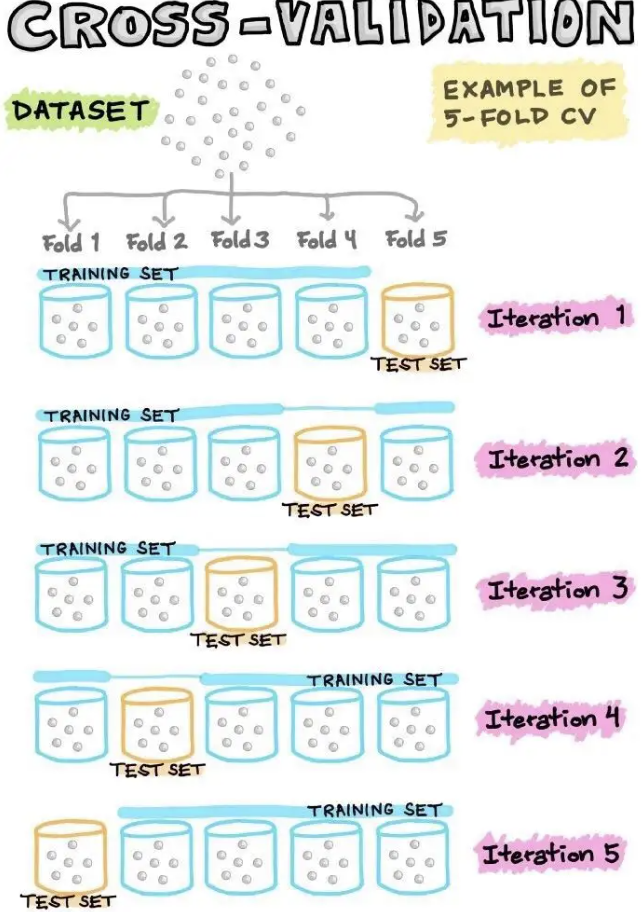
alt text

source:【绝对干货】机器学习模型训练全流程！- 知乎 https://zhuanlan.zhihu.com/p/184673895

留一法交叉验证 (Leave-one-out cross-validation)

留一法交叉验证是 K 折交叉验证的一个特例，当分折的数量K等于数据的数量n时，K 折留一法便成了留一法交叉验证。

  • 留一法交叉验证相较于普通的交叉验证方法，几乎使用了所有数据去训练模型。

  • 留一法交叉验证 (Leave-one-out cross-validation)的缩写为 loo-cv，或者 loo。

ELPD (Expected log-predictive density)

留一法交叉验证 LOO (包括之前的交叉验证方法)是用于评估模型在未知数据上预测能力的思想框架，其本身并不提供具体的统计指标。

ELPD (Expected log-predictive density) 是 LOO 方法的具体实现，以对数似然函数作为统计指标。

其计算步骤：

  • 同 K 折交叉验证一样，首先将数据集分成 n 份，n为数据总的数量。

  • 利用 n-1 份数据去训练模型，得到后验模型\(p(\theta_{-i}|y_{-i})\)

  • 使用剩下的一份数据作为测试数据\(y_i\)，计算后验预测模型\(p(y_i|y_{-i})\)

  • 重复以上过程 n 次，得到 n 个后验预测模型,并计算其对数化后的期望值\(E(log(p(y_i|y_{-i})))\)

alt text

补充：其他指标

之前讨论过模型评估中两种类型的指标：

  • 绝对指标，衡量模型对于样本的预测能力。

  • 相对指标，衡量模型对于样本外数据的预测能力，也考虑了模型的复杂度。

这两种指标包含了多种具体的统计值：

模型拟合优度的方法包括：

  • MAE or MSE(mean square error)

  • 对数似然 (log likelihood)

  • R²

模型预测进度的方法包括：

  • AIC

  • DIC

  • WAIC

  • LOO-CV

AIC

DIC

WAIC

LOOCV

BIC

适用框架

频率论

贝叶斯

贝叶斯

贝叶斯

贝叶斯/频率论

偏差（deviance）

最大似然参数\(\theta_mle\)的对数似然

贝叶斯参数均值\(\overline{\theta}\)的对数似然

LPPD

\(ELPD_{LOO-CV}\)

最大似然参数\(\theta_mle\)的对数似然

矫正

参数数量

似然的变异

似然的变异

由于采用LOO-CV的思想，因此不需要矫正

参数数量+数据数量

目前认知建模在科学心理学中得到了广泛应用，而模型比较作为认知建模的核心环节，不仅是评估模型对数据的拟合优度（平衡过拟合与欠拟合），还需要考虑模型复杂度对预测能力的影响。

然而，由于模型比较指标种类繁多，研究者在选用时往往面临困惑。

在郭鸣谦等(2024) 的文章中便把常用指标划分为三类，其中AIC、DIC、WAIC 等基于交叉验证的指标，通过数据分割或后验分布计算预测性能，平衡拟合优度和复杂度。

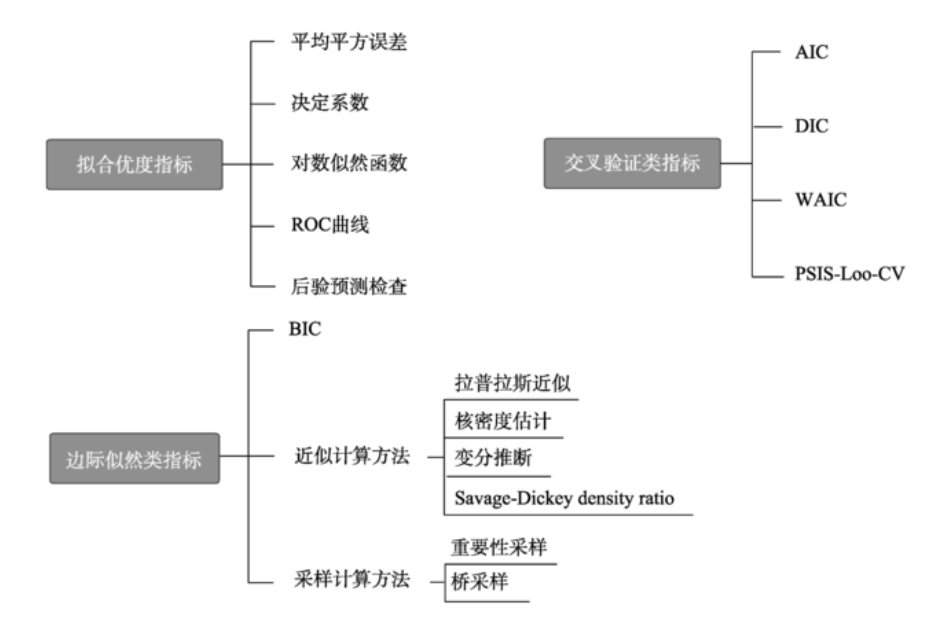
alt text

source: 郭鸣谦, 潘晚坷, 胡传鹏. (2024). 认知建模中模型比较的方法. 心理科学进展, 32(10), 1736-1756. doi: 10.3724/SP.J.1042.2024.01736

众多指标关心的核心问题：一个是它对于训练样本的预测能力如何；另一个则是它对样本外的预测能力如何。

  • 此外，近来也有研究者认为：不一定需要选出一个最优的指标，可以把所有合理的模型都纳入近来，然后对它们的预测进行加权平均，最后做出一个总的预测，也就是“模型平均”的思路。

偏差-方差权衡 (Bias-Variance Trade-off)#

  • 偏差（Bias）：指的是算法的期望预测与真实预测之间的偏差程度， 反映了模型本身的拟合能力，即模型本身对当前数据集的拟合偏差。

  • 方差（Variance）：与我们通常所说的方差有所不同，是指用不同训练数据进行模型评估时，模型表现的变化程度。

在模型训练过程中，偏差和方差之间存在一定的权衡关系：

  • 高偏差通常伴随着低方差，即模型较为简单，但能够在不同训练数据集上保持较为稳定的表现；

  • 低偏差通常伴随着高方差，即模型较为复杂，可以在训练数据上做得很好，但在其他数据集上表现不稳定；

因此，偏差和方差之间需要达到一种平衡，即偏差-方差权衡，以避免模型过于简单或过于复杂。

在模型评估中，无论是绝对评估还是相对评估，都可以结合偏差-方差权衡的概念来理解。偏差-方差权衡揭示了以下关键事实：

  • 模型越复杂：虽然能够更好地拟合训练数据，但往往会失去对样本外数据的解释能力（即过拟合）。

  • 模型越简单：尽管能够在不同样本间保持一致性，但对于任何特定样本的解释力可能较弱（即欠拟合）。

举例说明：

  • 如果我们的目标是建立一个能够准确预测响应变量 ( Y ) 的模型，就需要包含足够多的预测因子，以获得对 ( Y ) 的充分信息。

  • 然而，加入过多的预测因子可能适得其反。模型不仅会过度拟合训练数据，还可能导致复杂性增加，从而降低泛化能力。

通过平衡模型的偏差和方差，我们可以选择一个既能够捕捉数据结构，又具有良好预测能力的模型。这种权衡是建模过程中不可忽视的核心问题。

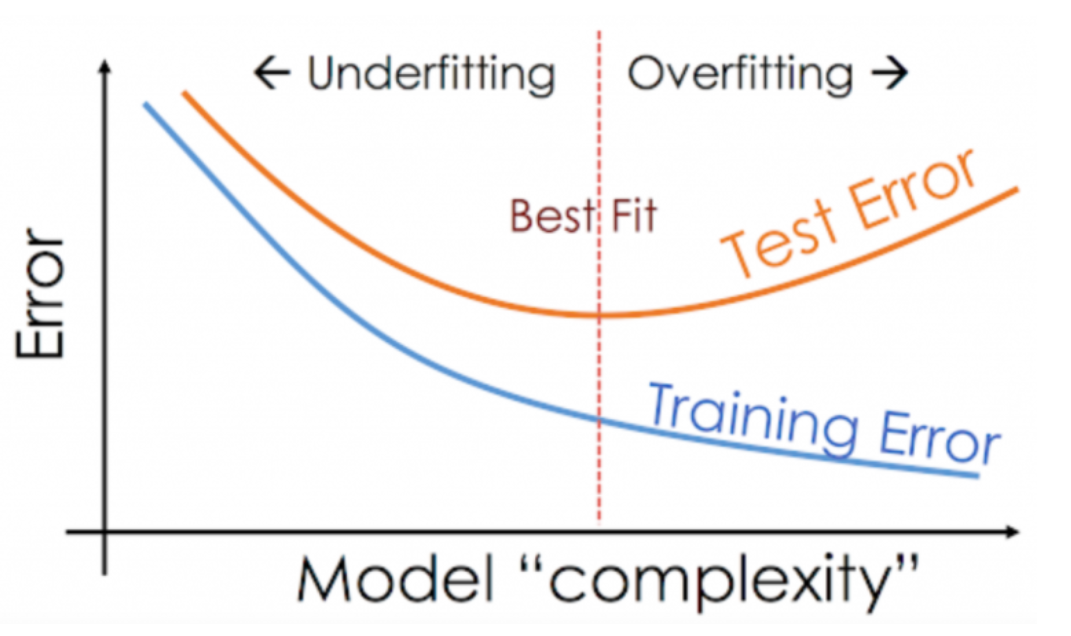
alt text

  • 模型评估的核心在于模型捕捉到了数据中的关键模式，既非太简单而错过数据中有价值的信息(欠拟合, underfitting)，也不会太复杂从而将数据中的噪音加入到模型中(过拟合, overfitting)。

欠拟合(underfitting)

欠拟合的模型在当前样本的数据拟合效果不好，且其泛化能力(模型在当前样本外新的数据上的预测的准确度)也同样不佳。

导致欠拟合的原因:

  • 数据特征较少

    • 数据特征指的是数据的属性，比如第一部分中展示的数据的各个变量就是数据的特征。在所有变量都能独立地对目标变量做出解释的前提下，数据特征越多，数据拟合程度越好。

  • 模型复杂度过低

    • 模型的复杂度代表模型能够描述的所有函数，比如线性回归最多能表示所有的线性函数。

    • 模型的复杂度和模型的参数数量有关，一般来说，模型参数越多，复杂度越高，模型参数越少，复杂度越低。

如何避免欠拟合

  • 增加数据的特征

  • 增加模型复杂度

过拟合(overfitting)

  • 模型在当前样本的数据上的拟合程度极好，但是泛化能力也较差。

  • 模型把训练样本学习地“太好了”，把样本自身地一些噪音也当作了所有潜在样本都会具有的一些性质，这样就会导致其泛化性能下降。

导致过拟合的原因

  • 当前样本的噪音过大，模型将噪音当作数据本身的特征

  • 当数据的有些特征与目标变量无关，这些特征就是噪音，但它也可能被误当作数据特征，这就会造成模型过拟合

  • 样本选取有误，样本不能代表整体

  • 模型参数太多，模型复杂度太高

如何避免过拟合

  • 选择更具代表性的数据

  • 降低模型复杂度

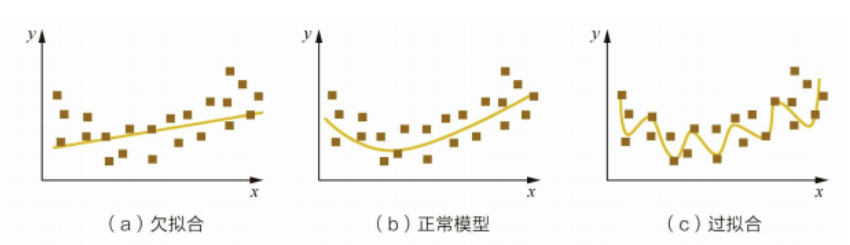
alt text

问题的本质在于：模型与数据真实的生成模型匹配

⚠需要注意：

在进行数据分析之前，一定要先看看原始数据长什么样，对原始数据进行可视化，而不是一上来就只看统计结果，这是一个很危险的做法。

模型评估指标的代码演示#

在我们了解模型评估的基本原理和方法后，接下来我们通过代码来演示如何使用这些方法来评估模型。包括：

  • 绝对指标，MAE

  • 相对指标，ELPD-LOO

计算MAE#

MAE是观测值(\(Y_i\))和后验预测均值(\(Y_i'\))的绝对误差的中位数，公式为：

\[ MAE = median(|Y_i-Y_i'|) \]

  • \(Y_i\):实际观测值

  • \(Y_i'\)：模型后验预测的均值

接下来我们通过代码来演示如何计算 MAE，以 model 1 为例。

1、提取后验预测数据，从模型中提取后验预测数据是后续计算的基础。

# 从采样结果中提取后验预测样本
posterior_predictive = model1_trace.posterior_predictive["Y_obs"]

# 在draw 和 chain 两个维度上计算后验均值
posterior_mean = posterior_predictive.mean(dim=["chain", "draw"])

posterior_mean.head()

2、计算 MAE

通过提取的后验预测值，计算 MAE，作为模型预测误差的绝对指标。

# 计算 MAE（观测值和后验均值的绝对误差的中位数）
mae = np.median(np.abs(df["RT_sec"] - posterior_mean))

print(f"MAE: {mae}")

3、对于 MAE 的解读。

  • 绝对误差的中位数，median absolute error (MAE)衡量了预测观测值\(Y_i\)与后验预测均值之间\(Y_i'\)的差异。

  • MAE越小表明后验模型的预测越准确。

我们可以对比三个模型的 MAE 结果:

def calculate_mae(trace, observed_data, dv = "Y_obs"):
    """
    计算后验预测均值和 MAE (Median Absolute Error)。
    
    Parameters:
    - trace: PyMC 模型的采样结果 (InferenceData 对象)。
    - observed_data: 包含真实观测值的 Pandas DataFrame。
    - dv: 需要计算 MAE 的数据列名，默认为 "Y_obs"。

    Returns:
    - posterior_mean: 后验预测值的均值。
    - mae: 后验预测均值与观测值之间的 MAE。
    """

    # 提取后验预测值
    posterior_predictive = trace.posterior_predictive[dv]
    
    # 计算后验预测均值（在 draw 和 chain 两个维度上取平均值）
    posterior_mean = posterior_predictive.mean(dim=["chain", "draw"])
    
    # 计算 MAE（绝对误差的中位数）
    mae = np.median(np.abs(observed_data - posterior_mean))
    
    return mae

pd.DataFrame({
    "Model 1": [calculate_mae(model1_trace, df["RT_sec"], "Y_obs")],
    "Model 2": [calculate_mae(model2_trace, df["RT_sec"], "Y_obs")],
    "Model 3": [calculate_mae(model3_trace, df["RT_sec"], "Y_obs")],
})

Model1:0.087913 ; Model2:0.088987 ; Model3:0.089136

计算ELPD-LOO#

在实际操作中，我们通过 ArViz 的函数az.loo计算\(ELPD_{LOO-CV}\)

  • 在az.loo返回的值中，elpd_loo为\(E(log(p(y_i|y_{-i})))\)

  • elpd_loo越高表示模型的预测值越精确

注意：由于\(ELPD_{LOO-CV}\)的计算量也比较大，ArViz 会使用 Pareto Smooth Importance Sampling Leave Once Out Cross Validation (PSIS-LOO-CV) 来近似。

PSIS-LOO-CV 有两大优势：

  • 计算速度快，且结果稳健

  • 提供了丰富的模型诊断指标

注意：

  • 要计算 elpd_loo 需要在采样 pm.sample 中加入 idata_kwargs={"log_likelihood": True}

  • 或者，在模型采样完成后计算对数似然，即 with model: pm.compute_log_likelihood(model_trace)。

首先，我们以 model 3为例

# 以 model 3 为例计算elpd_loo

az.loo(model3_trace)

alt text

  • 结果解读：

如果good的比例（pct.）非常高的话，我们可以认为这个ELPD-LOO的结果是可信的。如果bad或very bad的比例很高的话，那就意味着这个结果可能需要再谨慎考虑一下。

  • 然而，仅凭单个值，并不能反映模型的预测精确程度。

虽然 ELPDs 无法为任何单一模型的后验预测准确性提供可解释的度量，但它在比较多个模型的后验预测准确性时非常有用。

我们可以通过 arviz.compare 方法来对比多个模型的 elpd:

comparison_list = {
    "model1":model1_trace,
    "model2":model2_trace,
    "model3":model3_trace,
}
az.compare(comparison_list)

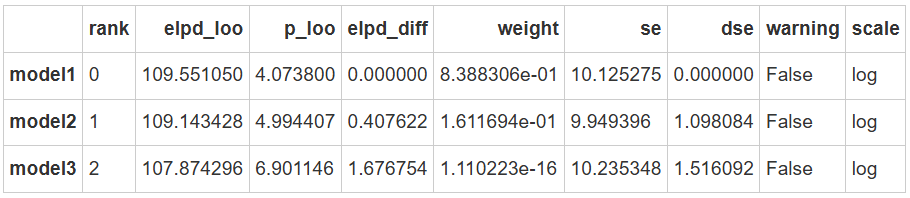
alt text

从结果可以看出：

  • 模型1的 elpd_loo 最大，表明它对样本外数据的预测性能最好。

  • 而模型3的 elpd_loo 最小，表明它的预测性能最差。

  • 并且这些结果与我们通过 MAE 计算及上节课的贝叶斯因子计算和HDI+rope 区间计算得到的判断一致。

需要注意的是：

  • arviz 提供的结果包括了 elpd se，这使得我们可以判断两个模型的预测差异 elpd_diff 是否超过两至三个标准误se。

补充：DIC在python中的实现#

DIC（Deviance Information Criterion）是用于模型选择和评估的指标，通常用于贝叶斯模型。在统计学中，DIC 是一种衡量模型拟合优度和复杂度的指标，类似于AIC（Akaike Information Criterion）和BIC（Bayesian Information Criterion）。

  • 在贝叶斯统计中，DIC 适用于基于 MCMC (Markov chain Monte Carlo) 采样估计的模型。

由于PyMc中没有直接计算DIC的方式，我们补充这一内容，方便同学们在练习中参考。

DIC的计算公式：

\[ DIC = -2D(\overline{\theta})+2×p_D \]

  • 其中，\(\overline{\theta}\)为参数后验分布的均值，而\(D(\theta)\)则是真实数据与模型预测分布之间的偏差（Deviance），用以衡量模型的性能。

  • DIC公式的第一项是-2乘上后验分布上的均值的偏差，代表了模型拟合的程度

  • 第二项\(p_D\)被称为有效参数（effective number of parameters），是模型拟合的复杂度的惩罚项，也就是将模型参数数量增加后所带来的拟合优势平衡一下。

DIC 综合考虑了模型的拟合优度和复杂度。模型的 DIC 值越低，说明模型在平衡拟合优度与复杂度后表现越好。

偏差的公式为：

\[ D(\theta_s)=logL(y|\theta_s) \]

  • 其中s代表了MCMC的样本，因此\(\theta_s\)是MCMC样本的参数值

有效参数\(p_D\)

\(p_D\)为有效参数(effective number of parameters), 是模型拟合的复杂度的惩罚项, 计算公式如下：

\[ p_D=Var(D(\theta))=\frac{1}{M}\sum\limits_{m=1}^{M}D(\theta^{(m)})-D(\hat{\theta}) \]

  • 其中，\(D(\theta^{(m)})\)是第m个样本的偏差，\(\hat{\theta}\)是后验均值

代码实现：

要根据模型的 log-likelihood 结果计算 DIC (Deviance Information Criterion)，可以按照以下步骤操作：

假设 model_trace.log_likelihood["Y_obs"] 是后验采样的 log-likelihood 值。

log-likelihood 的结构：

  • log_likelihood 是一个包含多个链和采样的对数似然值矩阵。

  • 在 chain 和 draw 维度上计算均值可以得到每个观测值的平均 log-likelihood。

首先，我们以model1为例进行演示

def calculate_dic(log_likelihood):
    """
    根据 log-likelihood 计算 DIC (Deviance Information Criterion)。 参考 Evans, N. J. (2019). Assessing the practical differences between model selection methods in inferences about choice response time tasks. Psychonomic Bulletin & Review, 26(4), 1070–1098. https://doi.org/10.3758/s13423-018-01563-9
    
    Parameters:
    - log_likelihood: xarray 数据集，包含每个链和样本的 log-likelihood 值。
    
    Returns:
    - dic: 计算得到的 DIC 值。
    """
    # 计算每个样本的Deviance
    deviance_samples = -2 * log_likelihood
    
    # 计算平均Deviance
    D_bar = deviance_samples.mean()
    
    # 计算有效自由度 p_D
    p_D = deviance_samples.max() - D_bar
    
    # 计算DIC
    DIC = -2 * (D_bar - p_D)
    
    return DIC["Y_obs"].values

# 调用 compute_dic 函数
dic_value = calculate_dic(model1_trace.log_likelihood)
print(f"DIC 值: {dic_value}")

同样我们可以计算所有模型（model1，model2，model3）的 DIC 值进行对比：

pd.DataFrame({
    "Model 1": [calculate_dic(model1_trace.log_likelihood)],
    "Model 2": [calculate_dic(model2_trace.log_likelihood)],
    "Model 3": [calculate_dic(model3_trace.log_likelihood)],
})

Model1

Model2

Model3

0

28.29209986121615

24.679373842803408

27.387719057819087

🤔思考：

1、如果你的目标是在不控制任何其他因素的情况下探索反应时间和什么有关，你会使用哪种模型？

  • 考虑到模型1优于模型2和模型3–因此，选择模型1可能能更好地反应反应时间的变化。

2、如果你的目标是最大限度地提高模型的预测能力，而在模型中只能选择一个预测因子，您会选择Label还是Matching？

  • 由于模型1优于模型2，如果仅选择一个预测变量的话，选择Label能获得对于反应时间更好的预测。

3、这四个模型中，哪个模型的总体预测结果最好？

  • 模型1以微弱优势超过了使用所有预测因子的模型2。这表明，在建立模型的过程中，预测因子并不是越多越好。

  • 事实上，模型3比模型2还差一点，这表明Label和matching之间的交互效应很弱，加入两者的交互项，会减弱模型的预测能力。

因此，为了简单高效，我们更有理由选择模型1。

alt text

Contents