Part 3: 后验模型#
当我们有了先验和似然两种信息,可以尝试进行推断后验:
\(ACC\sim Beta(70,30)\)
\(Y|ACC\sim Bin(50,ACC)\)
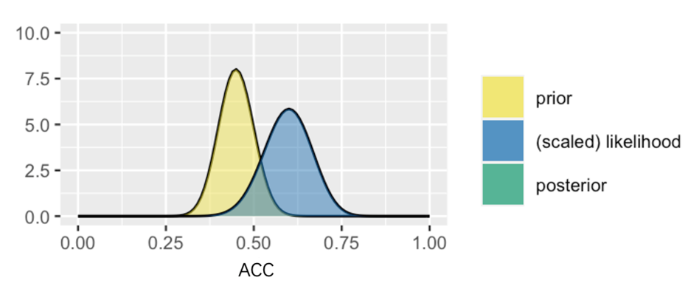
注意:在里面,为了方便在视觉上对比先验和似然,似然函数被缩放为相加和为1
思考🧐
哪一张图正确反映了后验模型?
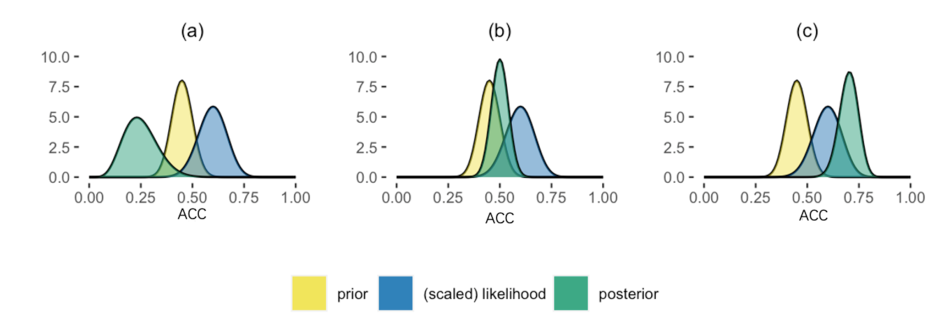
根据我们之前学的知识可知:贝叶斯推断是将先验和数据的信息组合起来进行的。数据和模型结合形成了likelihood,最后得到的后验实际上是对二者的加权。因此,根据我们的直觉来看,似乎图(b)更符合后验分布。
现在,我们通过实际计算绘制出后验图:
# 导入统计建模工具包 scipy.stats 为 st
import scipy.stats as st
# 设置 x 轴范围 [0,1]
x = np.linspace(0,1,10000)
# 设置 Beta 分布参数
a,b = 70,30
# 形成先验分布
prior = st.beta.pdf(x,a,b)/np.sum(st.beta.pdf(x,a,b))
# 形成似然
k = 30 # k 代表正确率为1的次数
n = 50 # n 代表总次数
likelihood = st.binom.pmf(k,n,x)
# 计算后验
unnorm_posterior = prior * likelihood # 计算分子
posterior = unnorm_posterior/np.sum(unnorm_posterior) # 结合分母进行计算
likelihood = likelihood /np.sum(likelihood) # 为了方便可视化,对似然进行类似后验的归一化操作
# 绘图
plt.plot(x,posterior, color="#009e74", alpha=0.5, label="posterior")
plt.plot(x,likelihood, color="#0071b2", alpha=0.5, label="likelihood")
plt.plot(x,prior, color="#f0e442", alpha=0.5, label="prior")
plt.legend()
plt.xlabel("ACC")
plt.fill_between(x, prior, color="#f0e442", alpha=0.5)
plt.fill_between(x, likelihood, color="#0071b2", alpha=0.5)
plt.fill_between(x, posterior, color="#009e74", alpha=0.5)
sns.despine()
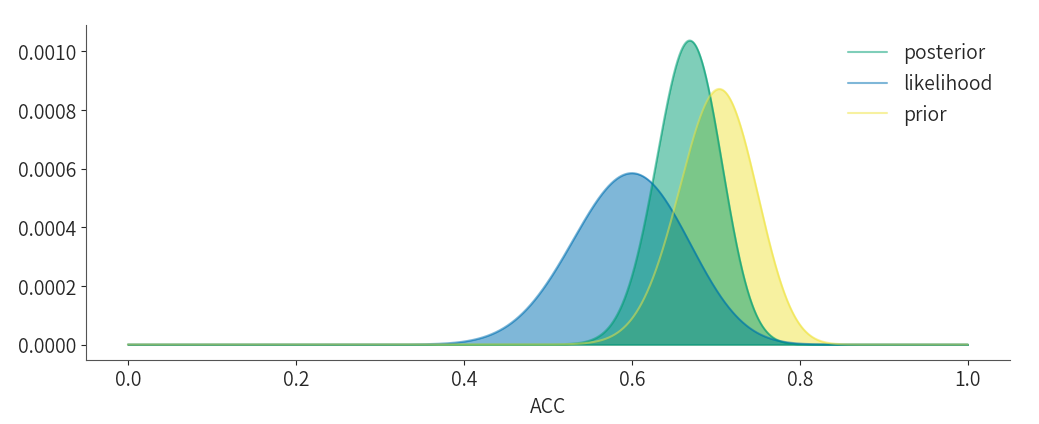
#-----------
正式计算
\(P(ACC|y=30)=\frac{P(ACC)L(ACC|y=30)}{P(y=30)}\)
和之前一样,分母\(P(y=30)\)是一个常数,在计算中可以将其忽略
\(P(ACC|y=30)\propto [\frac{Γ(100)}{Γ(70)Γ(30)}·(^{50}_{30})]·ACC^{69}(1-ACC)^{29}·ACC^{30}(1-ACC)^{20}\)
[ ]中的也是可以忽略的常数项
\(P(ACC|y=30)\propto ACC^{99}(1-ACC)^{49}\)
根据这个公式,我们发现\(P(\pi|y=30)\)和\(Beta(100, 50)\)有着相同的形状
\(Beta(100,50)=\frac{\Gamma(150)}{\Gamma(100)\Gamma(50)}\pi^{99}(1-\pi)^{49}\)
实际上,在这里后验分布也确实是Beta分布:
\(\pi|(Y=30)\sim Beta(100,50)\)
对后验模型进行总结
在结合先验和似然之后,我们对正确率ACC的认识发生了更新。
需要注意的是:后验模型仍然是一个\(Beta\)分布,和先验模型是同一个分布族。
\(ACC|(Y=30)\sim Beta(100,50)\)
\(f(ACC|y=30)=\frac{\Gamma(200)}{\Gamma(100)\Gamma(100)}ACC^{99}(1-ACC)^{99}\)
所以我们可以对二者进行对比,下表进行了这一总结,可以发现,在新的数据产生之后:
例如:
对正确率的期望值从0.70降低为0.67
模型的标准差从0.0657减少为0.0471
prior |
posterior |
|
|---|---|---|
\(\alpha\) |
70 |
100 |
\(\beta\) |
30 |
50 |
mean |
0.70 |
0.67 |
mode |
0.694 |
0.663 |
var |
0.00432 |
0.00222 |
sd |
0.0657 |
0.0471 |
上表可以看出,从先验到数据更新再到后验,无论是Beta分布的参数\(\alpha\)和\(\beta\),还是均值、众数以及方差、标准差都得到了更新。最重要的是我们发现方差实际上在变小,也就是说,得到数据前的估计存在一定的不确定性,而得到数据后,这种估计的不确定性在缩小——因为我们得到了一部分关于这个人的真实的数据。
思考🧐
先验分布的形态是否决定了后验分布的形态?(还记得之前关于正态分布和Beta分布的例子吗)
先验分布和后验分布是否必然一致?
