Leture6: MCMC

Leture6: MCMC#

在上一节课中，通过简单的 Beta-Binomial 模型中，我们已经看到 PyMC 可以帮助我们得到后验分布。

且这个过程中使用了MCMC算法从后验分布中进行抽样。

🤔思考：为什么MCMC算法可以得到后验分布的样本？Markov Chain Monte Carlo看起来分为两个部分，这两个部分到底是什么含义?

Monte Carlo, Markov Chain 和 Markov Chain Monte Carlo#

什么是 Monte Carlo ?#

🤔问题：假设我们知道这个正方形的面积，想估算图中圆形的面积（但不使用圆的面积的公式），通过何种近似的方法可以怎么解决这一问题呢？

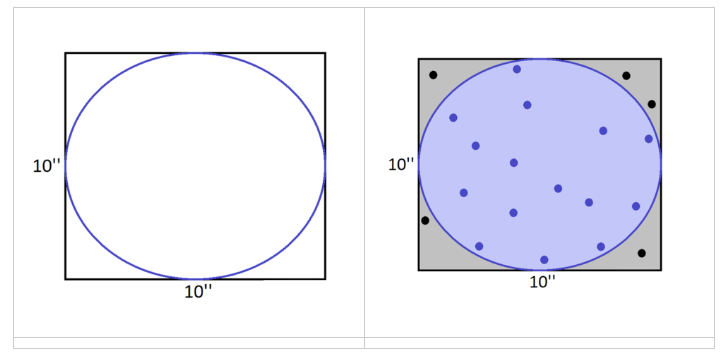
alt text

  • 思路：假设我们向这个正方形内随机抛入一些点，并且这些点落在这个空间当中的概率是均等的，那么就意味着它落在这个圆里和落在圆外的数量应当是成比例的。既然这样的话，那么落在圆里的点的数量与总数量之比，大概就是这个圆和整个正方形的面积之比。

步骤

1.随机投点：我们在一个边长为 10 英寸 的正方形区域内随机放置 20 个点。

2.计算圆内的点数比例：统计这些点中有多少落在圆内，并计算这一比例。

3.面积估算：根据比例，乘以正方形的面积（100 平方英寸），即可得到近似的圆面积。

Monte Carlo 的核心思想：

  • 随机抽样：通过从某个已知的概率分布中随机抽样，估计该分布的期望或其他统计量。

  • 近似逼近：随着样本数量增加，抽样结果会逐渐逼近真实分布的统计特性。

Normal-Normal 模型的后验分布

接下来，我们使用正态模型为例进行演示。（贝叶斯中，我们使用Normal-Normal表示先验与似然都是Normal Dist）

  • 假设我们知道一个正态分布的标准差为0.75，但是其平均值\(μ\)是未知的，我们想通过从这个正态分布中取一个数据来估计这个正态分布的平均值\(μ\)的范围。

1.似然模型：假设我们从一个平均值为\(μ\)，标准差为0.75的正态分布中获取了一个\(Y=6.25\) 的数据：

\[ Y|\mu \sim N(\mu,0.75^2) \]

2.先验模型：假定这个正态分布的均值是可能是从如下正态分布中取值的：

\[ \mu \sim N(0,1^2) \]

可以简单理解为我们一开始对\(\mu\)的信念，在均值为0，标准差为1的正态分布中波动。

3.后验分布：那么在\(Y=6.25\)的结果下，结合先验，更新后的\(\mu\)是怎样的呢？

\[ \mu|(Y=6.25) \sim N(?,?) \]

后验分布解析解：

由于Normal-Normal为共轭先验，我们可以用公式直接计算出它的后验分布：

\[ \mu|\overrightarrow{y} \sim N(\frac{\theta \sigma^2+\overline{y}nr^2}{nr^2+\sigma^2},\frac{r^2\sigma^2}{nr^2+\sigma^2}) \]

其中：

  • \(\overline{y}\)是样本的均值，即观察到的平均正确率

  • \(\sigma^2\)是已知的正确率方差

  • \(r^2\)是先验的方差

  • 后验均值：后验均值是先验均值\(\theta\)和样本均值\(\overline{y}\)的加权平均：

\[ posterior ~ mean = \frac{0×0.75^2+6.25×1^2}{1^2+0.75^2}=4 \]

  • 后验方差：后验方差受先验方差\(r^2\)和样本数据的方差\(\sigma^2\)的共同影响：

\[ posterior ~ variance=\frac{1^2×0.75^2}{1^2+0.75^2}=0.6^2 \]

因此，我们通过解析解的方式得到了更新后的\(\mu\)的分布为：

\[ \mu|(Y=6.25) \sim N(4,0.6^2) \]

后验分布模型 vs. 从后验分布采样#

💥需要区分清楚两个概念：

通过解析计算得到的后验分布模型 与 从后验分布中得到的采样结果 并不完全相同

例如，虽然我们通过解析计算得到了后验分布的具体形式，但这并不意味着我们获得了这个\(\mu\)的采样。

为了获得这些样本（sample），我们需要通过Monte Carlo过程采样。

  • 简单地说：我们希望得到的样本的数量与每个样本在分布模型中的可能性之间是成比例的，某个值出现的概率越大，在采样中，它出现的次数应该越多。

  • 反过来说，如果我们能从某个分布中采到足够多的样本，那么我们也可以通过对这些样本的统计量进行计算，来估计这个分布本身的模型参数。这就类似于我们一开始举的例子，我们从正方形内随机采样足够多的点，那么我们就可以根据点的数量比例来估计圆的面积。

Monte Carlo采样与可视化

在现代的概率编程语言中，我们很容易进行Monte Carlo采样。例如，对于上述的正态分布\(N(4,0.6^2)\)，我们可以通过以下代码对这一采样过程进行可视化。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

x_range = np.linspace(2, 10, 1000)       # 设置 x 的范围为 [2,10]，总共取1000个数 
y_reg = 6.25 * x_range + 0.75  #斜率为6.25，截距为0.75的一元线性
#y_norm为一个符合正态分布的概率密度函数，均值为6.25，标准差为0.75
y_norm = norm.pdf(x_range, 6.25, 0.75) 

# 对y_norm进行采样，得到1000个样本值
samples = np.random.normal(6.25, 0.75, 1000)

# 显示前 10 个样本值
first_10_samples = samples[:10]
print("前 10 个样本值：", first_10_samples)

这里显示出：前10个样本值： [7.82106053 5.84653561 5.51158156 6.38897953 7.6325137 5.08262722 6.76971937 7.50396243 7.28796121 5.31063869]

我们观察前10个样本值，大概也是围绕6.25这个均值分布的。现在我们将它用直方图可视化出来，观察采样形成的分布和使用解析解计算得到的分布是否相似。

#  绘制图像
plt.figure(figsize=(10, 6))
#plt.plot(x,y)
plt.plot(x_range, norm.pdf(x_range, 6.25, 0.75), linewidth=2, color='r', label='Normal Distribution PDF')
count, bins, ignored = plt.hist(samples, bins=30, density=True, alpha=0.6, color='grey', edgecolor='black', label='Sampled Histogram')

plt.legend()
plt.show()

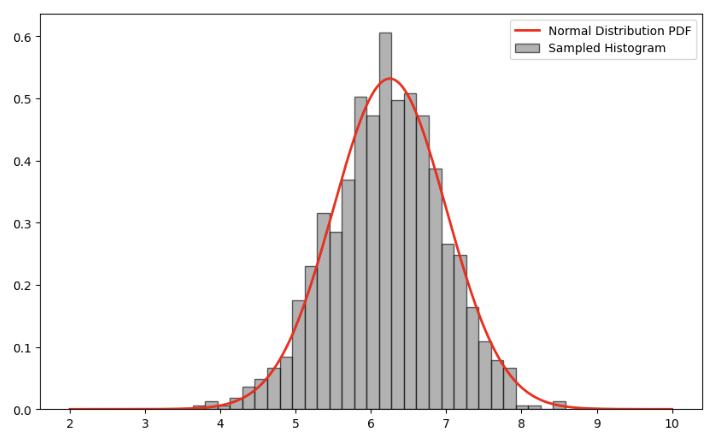
alt text

我们观察发现，二者形状大致相同，并且6.25这个位置采样的次数确实是最多的。

🤔现在我们思考一个问题：是不是通过Monte Carlo采样就可以直接得到后验呢？

未归一化的后验分布(unnormalized posterior pdf)

我们在上节课讲到，在现实的数据分布中，往往模型比较复杂，导致我们进行的计算变得复杂，尤其是分母部分的归一化因子。我们需要将所有可能的参数取值情况下的likelihood的值全部求出来，这个时候就会变得很复杂。

❓为什么归一化因子比较难以计算？

假如归一化因子（分母）比较难以计算，是不是可以不计算？

alt text

Q: 假如我们只知道上面随机点的信息，但不知道正方形的面积，我们如何估算圆的面积？

A: 使用足够多的点，计算圆内点的比例

  • 对于贝叶斯推断来说，我们可能可以不用计算归一化因子，直接通过对后验分布的采样来近似得到后验分布。

\[ f(\mu|y=6.25) \sim f(\mu)L(\mu|y=6.25) \]

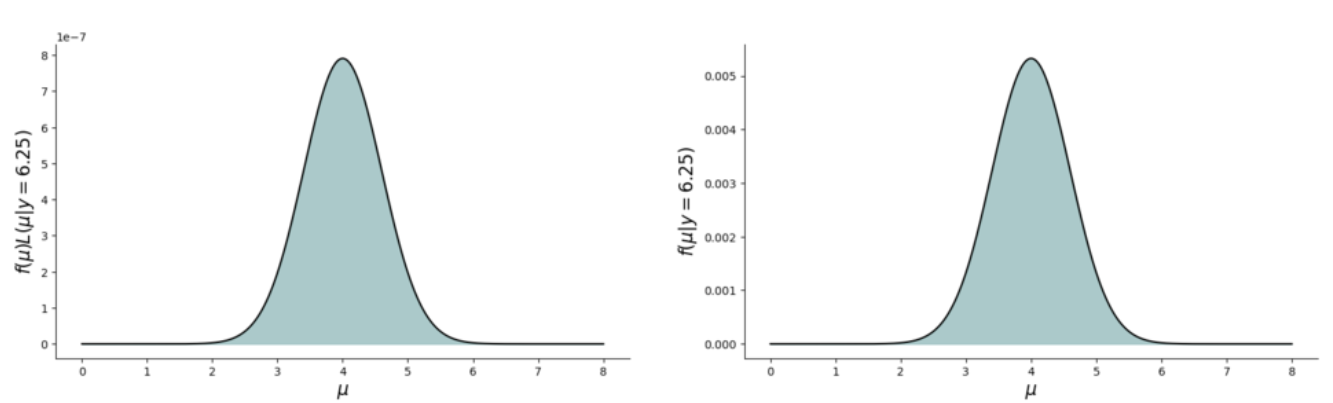
  • 尽管未归一化的分布并不是真正的后验分布，但这二者的形状、集中趋势、变异性是一样的

  • 可以看到，真实的后验分布和未归一化后验分布，除了在 y 轴上的单位不一样，但他们的形状、集中趋势、变异性是一样的

  • 重要的是，两个分布中，\(μ\)的结果主要集中在 2-6 之间

因此，当进行采样时，我们可以使用未归一化的后验分布的结果来替代计算真实的后验分布\(f(\mu)\)

alt text

🤔思考：如何在不计算复杂归一化常数的情况下，有效地生成样本？

Markov Chain Monte Carlo#

Markov Chain（马尔可夫链）即可自然地解决了未归一化的后验分布的问题。

原因：

  • 每次只关注当前的状态。

  • 利用当前状态生成建议分布（proposed distribution）。

  • 判断是否接受新的状态，构建一个链条来近似后验分布。

我们以一个心情变化的例子来深入理解 Markov Chain：

  • 假如不同的情绪对应一种状态，也就是参数可能的取值。

  • 那么，我们可以将不同的心情（如“冷静”、“悲伤”、“开心”）定义为 状态。这些状态中的每一个代表参数\(\theta_k\)的不同取值：

  • 例如，冷静是\(\theta_1=0.5\); 悲伤是\(\theta_2=0.3\)；开心是\(\theta_3=0.7\)； 以此类推…..。

  • 这样，我们可以确定参数选择的范围\(\theta_k \sim [0,1]\)，参数是离散变量，每一个值对应一种心情。

  • 注意，我们用下标 k 来表示不同的心情以及对应的参数值。

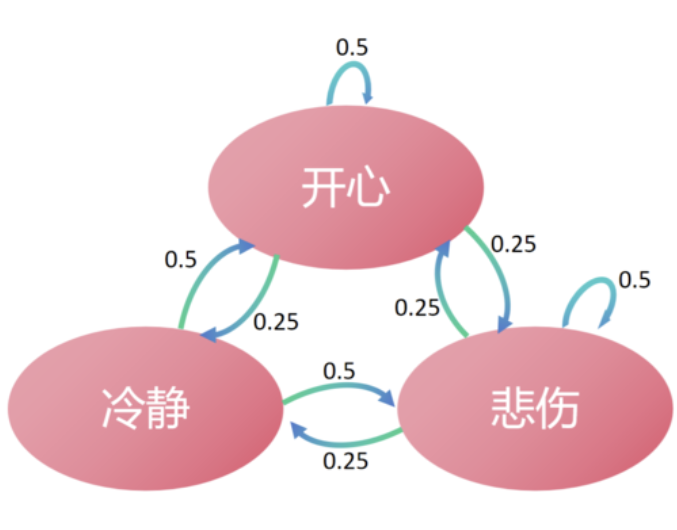
alt text

  • 状态转移：每一天我们的心情都会发生变化或者不变，代表一次采样，即一次状态的转移。

  • 长时间的跟踪这些状态，我们会得到一个马尔科夫链：{\(\theta^{(1)},\theta^{(2)},.....\theta^{(n)}\)}，这里n表示天数，\(\theta^{(n)}\)是第n天的具体心情。

  • 无记忆性：无记忆性是马尔可夫链的关键特点,今天的心情（当前状态）只依赖于昨天的心情（前一状态）。

例如，如果前一天是开心，那么今天继续保持开心的概率是0.5，而变为冷静或悲伤的概率均是0.25。

心情

开心\(\theta_1^{(n-1)}\)

冷静\(\theta_2^{(n-1)}\)

悲伤\(\theta_3^{(n-1)}\)

…

开心\(\theta_1^{(n)}\)

0.5

0.25

0.25

…

冷静\(\theta_2^{(n)}\)

0.5

0

0.5

…

悲伤\(\theta_3^{(n)}\)

0.25

0.25

0.5

…

解释：

  • 每一行代表当前状态影响下一状态的概率，也就是 当日心情(n)受到上一天心情(n-1)的影响。

  • 可以写成服从概率分布的形式：\(choice(n) \sim Distribution(n-1)\)

这里的Distribution 就是建议分布，它为第二天的心情变化提供了建议，所以被称为建议分布\(q(x)\)，并且根据这个分布来选择是否接受新的状态。

马尔可夫链的的好处：当我们运行一段时间后，会发现慢慢会稳定在某个状态，高概率的更多出现，低概率的情况更少出现。随着马尔可夫链迭代一段时间后，模型会慢慢稳定，并逐渐收敛到后验概率的真实情况

为什么 Monte Carlo 需要加上 Markov Chain？#

原因：

1.Monte Carlo 方法通过从目标分布中直接采样，使用大量随机样本来逼近期望值或目标概率。这种方法在低维分布中工作良好，但在高维复杂分布中直接采样变得非常困难和不现实。

2.为了解决高维空间中的采样困难，MCMC 使用马尔可夫链生成样本。每次样本的生成只依赖于前一次的状态，因此构建了一个可以逐渐收敛于目标分布的链条。

所以，MCMC 的核心思想即：

  • 构建一个符合目标分布的马尔可夫链：

每次新样本的生成依赖于前一个状态，逐步逼近目标分布。

  • 长时间采样达到平稳分布：

当马尔可夫链达到稳态分布时，采样结果便可以作为目标分布的近似。

尽管 MCMC 的实现方式多种多样，但所有方法的目标都是构建一个符合目标后验分布的马尔可夫链。许多 MCMC 算法，如吉布斯采样、差分进化算法 以及 PyMC 默认使用的 NUTS（No-U-Turn Sampler），都是 Metropolis-Hastings 算法的变种。

我们将在本节课重点讨论 Metropolis-Hastings (MH) 算法，通过对MH算法内部原理的学习，我们能够更容易理解MCMC的工作原理，有助于在后续实践过程中发现问题和解决问题。

  • 虽然实现该算法需要计算机编程技能，而这些技能并不在本课程的范围之内（例如编写函数和 for 循环），

  • 😜ps. 即使没有学会 MH 算法的实现，也不妨碍我们通过 pymc 来实现各种 MCMC 算法

Contents