练习

练习#

在以下的练习中，我们需要采用上述的思路，在另一个问题情境下使用贝叶斯的线性回归来解决问题。

背景介绍

  • 🤦‍♀️🤦‍♀️当你压力大时，或许也曾：疯狂购物、沉迷游戏；但有的时候，当你感觉到压力大时，或许也曾：卸载软件，聚精会神

  • 从直觉上我们能感受到似乎压力与自我控制之间存在某种联系

我们使用的数据来自Human Penguin Project (Hu et al., 2018, doi: 10.17605/OSF.IO/H52D3)，该项目使用了多种常见的心理测量量表，并在跨国人群中进行施测，其中包含了测量压力与自我控制的量表。

  • 测量压力的量表共有14道题，每道题的标尺有5个水平，分值为1-5，总分的分布范围为14-70

  • 测量自我控制的量表共有13道题，每道题的标尺有5个水平，分值为1-5，总分的分布范围为13-65

  • 数据来源: Hu, C.-P. et al. (2018). Raw data from the Human Penguin Project. Open Science Framework. https://doi.org/10.17605/OSF.IO/H52D3

  • 压力量表来源：Cohen, S., Kamarck, T. & Mermelstein, R. A global measure of perceived stress. J. Health. Soc. Behav. 24, 385–396 (1983).

  • 自我控制量表来源：Tangney, J. P., Baumeister, R. F. & Boone, A. L. High self-control predicts good adjustment, less pathology, better grades, and interpersonal success. J. Pers. 72, 271–324 (2004).

使用线性模型表示二者关系

  • 在这个例子中，我们将每个被试的自我控制水平设为\(Y\)，压力水平设为\(X\)。在收集完n个被试的数据后，我们可以得到：

\[ \{(Y_1,X_1),(Y_2,X_2),....,(Y_n,X_n)\} \]

  • 我们可以使用线性模型来描述\(Y\)与\(X\)的关系，常见地，我们会将二者的关系写为：

\[ Y_i=\beta_0+\beta_1X_{i1}+\epsilon~~\epsilon \sim N(0,\sigma^2) \]

设置先验

\[\begin{split} Y_i \sim N(\mu_i,\sigma^2)\\ \sigma \sim Exp(0.6)\\ \beta_0 \sim N(50,10^2)\\ \beta_1 \sim N(0,10^2) \end{split}\]

定义回归模型：

\[ \mu_i=\beta_0+\beta_1X_i \]
import numpy as np
import pandas as pd
import pymc as pm
import arviz as az

# 通过 pd.read_csv 加载数据 Data_Sum_HPP_Multi_Site_Share.csv
try:
    df_re = pd.read_csv('/home/mw/input/bayes3797/Data_Sum_HPP_Multi_Site_Share.csv')
except:
    df_re= pd.read_csv('data/Data_Sum_HPP_Multi_Site_Share.csv')


# 筛选站点为"Tsinghua"的数据
df = df_re[df_re["Site"] == "Tsinghua"]

df = df[["stress","scontrol","smoke"]]

#1 表示吸烟，2表示不吸烟
df["smoke"] =  np.where(df['smoke'] == 2, 0, 1)
df["smoke_recode"] =  np.where(df['smoke'] == 1, "yes", "no")


#设置索引
df["index"] = range(len(df))
df = df.set_index("index")

任务1：根据数据和模型定义 PyMC 模型

with pm.Model() as model4:
    
    ##---------------------------
    #     定义参数先验，包括 beta_0，beta_1，sigma
    #---------------------------
    beta_0 = ...          
    beta_1 = ...
    sigma = ...


    x = pm.MutableData("x",df.stress)                    #x是自变量压力水平
    ##---------------------------
    #     定义回归模型
    #---------------------------
    mu = ...                              

    ##---------------------------
    #     定义似然函数
    #---------------------------
    likelihood = ...

任务2：拟合模型并进行 MCMC 检查

##---------------------------
#     对模型 model4 进行 MCMC 采样
#---------------------------
...

##---------------------------
#     通过可视化+统计指标检验 MCMC 是否收敛
#     提示：可以使用 az.az.plot_trace() 和 az.summary()函数
#---------------------------
...

任务3：使用 HDI 或者 BF 进行模型推断

##---------------------------
#     参考前面的代码计算 HDI + ROPE 区间 或者贝叶斯因子计算
#---------------------------
...

任务4：进行后验预测

##---------------------------
#     对模型进行后验预测
#---------------------------
with model4:
    model4_ppc = ...

##---------------------------
#     可视化后验预测结果
#     提示：可以使用 az.plot_ppc(...)
#---------------------------
...

模型5：增加预测变量

🤔 是否可以将吸烟情况和压力同时加入到目前的模型4中?

如果我们现在将吸烟情况加入到目前的模型中的话，我们的线性回归模型则会更新为：

\[\begin{split} Y_i=\beta_0+\beta_1X_{i1}+\beta_2X_{i2}+\epsilon\\ \epsilon \sim N(0,\sigma^2) \end{split}\]

  • \(X_{i1}\)是第i个被试的压力水平；

  • \(X_{i2}\)是第i个被试的吸烟状态，\(X_{i2}=0\)表示不吸烟，\(X_{i2}=1表示吸烟\)

各参数(回归系数)的意义：

现在的例子中，自变量包括离散变量和连续变量。

在自变量中，\(X_{i2}\)为离散变量，0 表示不吸烟，1表示吸烟

  • 当\(X_{i2}=0时，\mu_i=\beta_0+\beta_1X_{i1}+\beta_2·0=\beta_0+\beta_1X_{i1}\)

表示不吸烟情况下，自我控制分数随压力分数变化的情况，二者的关系可以被简化为一条直线。

  • 当\(X_{i2}=1时，\mu_i=\beta_0+\beta_1X_{i1}+\beta_2·1=(\beta_0+\beta_2)+\beta_1X_{i1}\)

表示吸烟情况下，自我控制分数随压力分数变化的情况。

注意，在该模型中，我们假设在两种吸烟条件下，压力对自我控制的影响是相同的，即不存在吸烟对于压力的调节作用。

先验设置

\[\begin{split} Y_i \sim N(\mu_i,\sigma^2)\\ \sigma \sim Exp(0.6)\\ \beta_0 \sim N(50,10^2)\\ \beta_1 \sim N(0,10^2) \beta_2 \sim N(0,10^2) \end{split}\]

定义回归模型：

\[ \mu_i=\beta_0+\beta_1X_{i1}+\beta_2X_{i2} \]

任务1：根据数据和模型定义 PyMC 模型

with pm.Model() as model5:
    ##---------------------------
    #     定义参数先验，包括 beta_0，beta_1，sigma
    #---------------------------
    beta_0 = ...          
    beta_1 = ...
    beta_2 = ...
    sigma = ...


    stress = pm.MutableData("stress",df.stress, dims="obs_id")      #stress是自变量压力水平
    smoke = pm.MutableData("smoke",df.smoke, dims="obs_id")         #smoke是自变量吸烟水平
    ##---------------------------
    #     定义回归模型
    #---------------------------
    mu = pm.Deterministic("mu", ..., dims="obs_id")    #定义mu，自变量与先验结合

    ##---------------------------
    #     定义似然函数
    #---------------------------
    likelihood = pm.Normal("y_est", mu=..., sigma=..., observed=..., dims="obs_id")

任务2：拟合模型并进行 MCMC 检查

##---------------------------
#     对模型 model5 进行 MCMC 采样
#     注意！！！以下代码可能需要运行1-2分钟左右
#---------------------------
...

##---------------------------
#     通过可视化+统计指标检验 MCMC 是否收敛，，当你顺利运行了这段代码，可以举手示意助教/老师帮助你检查其模型建立的是否正确
#     提示：可以使用 az.az.plot_trace() 和 az.summary()函数
#---------------------------
...

任务3：使用 HDI 或者 BF 进行模型推断

##---------------------------
#     参考前面的代码计算 HDI + ROPE 区间 或者贝叶斯因子计算
#---------------------------
...

任务4：进行后验预测

##---------------------------
#     对模型进行后验预测
#---------------------------
with model5:
    model5_ppc = ...

##---------------------------
#     可视化后验预测结果
#     提示：可以使用 az.plot_ppc(...)
#---------------------------
...

多元线性回归：增加交互项

现在，我们可以假设，在不同的吸烟状况下，压力对自我控制的影响略有不同(体现在斜率上)

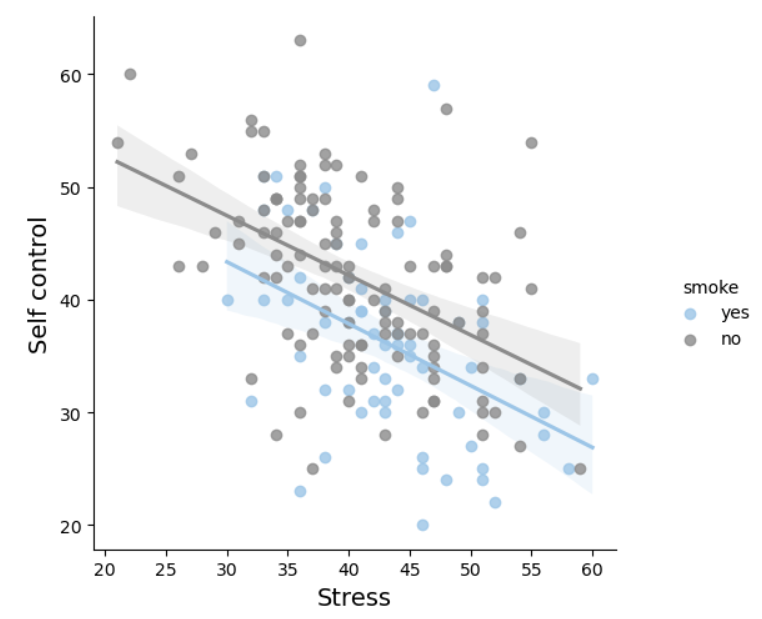
alt text

我们加入交互项：

\[ \mu_i=\beta_0+\beta_1X_1+\beta_2X_2+\beta_3X_1X_2 \]

交互项的先验：

\[ \beta_3 \sim N(0,10^2) \]

在这个例子中，各参数的意义：

  • 当\(X_{i2}=0时，\mu_i=\beta_0+\beta_1X_{i1}\)

表示不吸烟情况下，自我控制分数随压力分数变化的情况，二者的关系可以被简化为一条直线。

  • 当\(X_{i2}=1时，\mu_i=\beta_0+\beta_1X_{i1}+\beta_2X_{i2}+\beta_3X_{i1}=(\beta_0+\beta_2)+(\beta_1+\beta_3)X_{i1}\)

表示吸烟情况下，自我控制分数随压力分数变化的情况

注意截距项和斜率项的变化

此时压力对自我控制的影响为\((\beta_1+\beta_3)\)，体现了吸烟对这一关系的影响

任务1：根据数据和模型定义 PyMC 模型

with pm.Model() as model6:
    
    ##---------------------------
    #     定义参数先验，包括 beta_0，beta_1，sigma
    #---------------------------
    beta_0 = ...       
    beta_1 = ...
    beta_2 = ...
    beta_3 = ...
    sigma = ...

    stress = pm.MutableData("stress",df.stress, dims="obs_id")      #stress是自变量压力水平
    smoke = pm.MutableData("smoke",df.smoke, dims="obs_id")         #smoke是自变量吸烟水平
    ##---------------------------
    #     定义回归模型
    #---------------------------
    mu = pm.Deterministic("mu", ..., dims="obs_id")      #定义mu，将自变量与先验结合

    ##---------------------------
    #     定义似然函数
    #---------------------------
    likelihood = pm.Normal("y_est", mu=..., sigma=..., observed=..., dims="obs_id")

任务2：拟合模型并进行 MCMC 检查

##---------------------------
#     对模型 model6 进行 MCMC 采样
#     注意！！！以下代码可能需要运行1-2分钟左右
#---------------------------
...

##---------------------------
#     通过可视化+统计指标检验 MCMC 是否收敛，当你顺利运行了这段代码，可以举手示意助教/老师帮助你检查其模型建立的是否正确
#     提示：可以使用 az.az.plot_trace() 和 az.summary()函数
#---------------------------
...

任务3：使用 HDI 或者 BF 进行模型推断

##---------------------------
#     参考前面的代码计算 HDI + ROPE 区间 或者贝叶斯因子计算
#---------------------------
...

任务4：进行后验预测

##---------------------------
#     对模型进行后验预测
#---------------------------
with model6:
    model6_ppc = ...

##---------------------------
#     可视化后验预测结果
#     提示：可以使用 az.plot_ppc(...)
#---------------------------
...