Lecture14 : Hierarchical Regression Models

Lecture14 : Hierarchical Regression Models#

Intro#

在上一节课中，我们学习了分层模型 (Hierarchical Models) 的基本概念，并探讨了分层模型的应用，然而这些模型没有考虑实验条件的影响。

因此，为了检验实验条件在每个被试中的效应大小，需要结合回归分析方法。

  • 本节课将分层模型与回归模型相结合，重点讲解分层线性模型 (Hierarchical Regression Models) 的应用。

在前几次课的练习中讨论了“压力与自我控制关系”的例子，本节课将以该例子介绍分层线性模型的基本概念，在练习阶段时再回到随机点运动范式的情境。

alt text

alt text

在上节课的练习中仅考虑了自我控制分数在不同站点和不同个体间的变化。

🤔 然而，我们更想回答的问题是，压力对自我控制的影响是否在不同站点间存在差异？

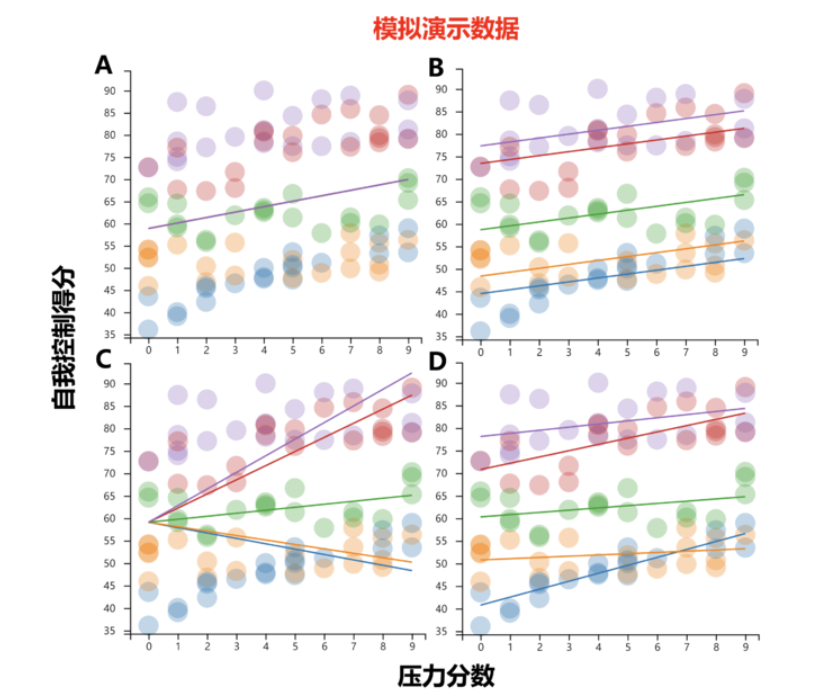
alt text

  • 如图A：一种不太可能的情景是，不同站点间的自我控制分数没有差异，并且压力对自我控制的影响在不同站点间也相同。

  • 如图B：一种可能是，自我控制分数在不同站点间存在差异，但是压力对自我控制的影响在不同站点不存在差异。

  • 如图C：另一种可能是，站点只调节压力对自我控制的影响，而各站点间自我控制分数相当。

  • 如图D：最后，站点可能既影响自我控制分数，又影响压力对自我控制的效应。

在本节课中，将介绍引入包含自变量时的分层模型，并通过不同的模型验证不同的假设：

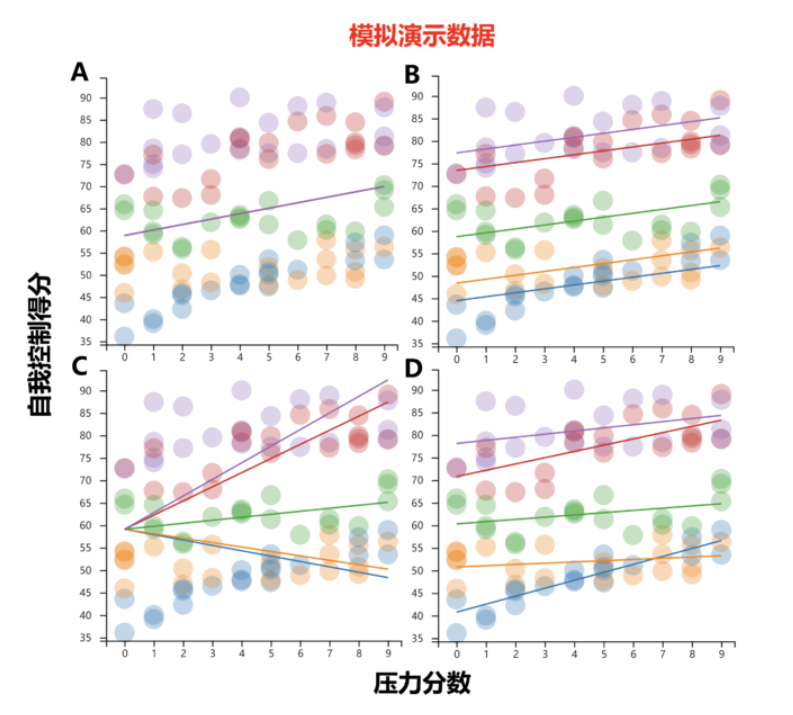
alt text

  • \(H_0(model 0)\)，图A，普通线性模型，仅考虑压力对自我控制的影响。

  • \(H_1(model 1)\)，图B，变化截距模型(斜率相同)，在模型0的基础上考虑自我控制在不同站点的变化。

  • \(H_2(model 2)\)，图C，变化斜率模型（截距相同），在模型0的基础上不同站点间的压力影响的变化。

  • \(H_3(model 3)\)，图D，变化截距和斜率模型，结合模型1和模型2，同时考虑站点对自我控制以及压力影响的变化。

回顾：贝叶斯回归模型的数学表达式

\[\begin{split} \beta_0 \sim N(m_0,s_0^2)\\ \beta_1 \sim N(m_1,s_1^2)\\ \sigma \sim Exp(\lambda)\\ \downarrow\\ \mu_i=\beta_0+\beta_1X_i\\ \downarrow\\ Y_i|\beta_0,\beta_1,\sigma \sim N(\mu_i,\sigma^2) \end{split}\]

回归模型需满足如下假设：

  • 独立观测假设：每个观测值\(Y_i\)是相互独立的。

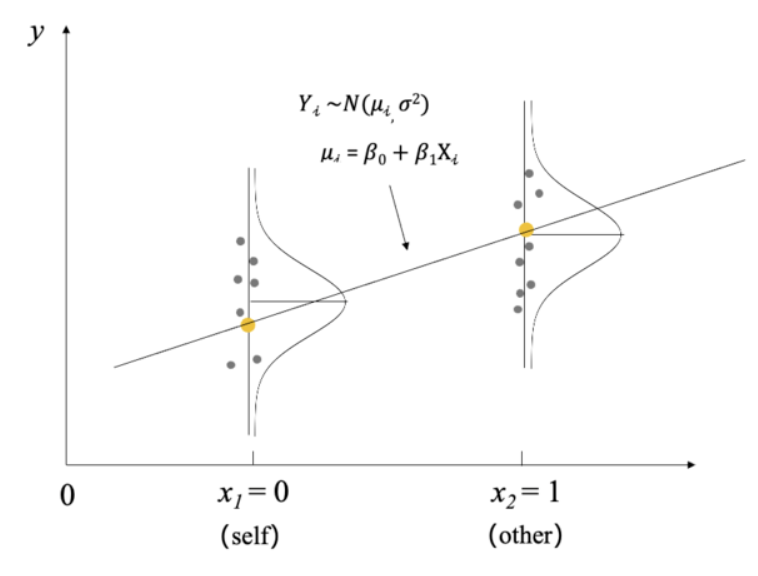
  • 线性关系假设：预测值\(\mu_i\)和自变量\(X_i\)之间可以用线性关系来描述，即：\(\mu_i=\beta_0+\beta_1X_i\)

  • 方差同质性假设：在任意自变量的取值下，观测值\(Y_i\)都会以\(\mu_i\)为中心，以相同的标准差\(\sigma\)呈正态分布变化。

贝叶斯回归模型的优势：

允许将实验假设以回归参数的形式进行表达，并通过后验分布来量化这些假设的合理性。

\[ RT_{sec} \sim N(\beta_0+\beta_1·Label,\sigma^2) \]

  • 通过后验分布检验\(\beta_1\)是否显著，例如计算\(\beta_1>0\)或\(\beta_1<0\)的概率，计算最高密度区间HDI。如果95%HDI不包含0，可以认为自我条件和他人条件在反应时上的差异是显著的。

  • 在贝叶斯框架下，不仅可以观察参数的点估计（如\(\beta_1\)的均值），还可以通过后验分布和 HDI 提供更加直观的置信水平解释。

alt text

Model0: Complete pooling#

以 “压力与自我控制关系” 为例， 如果忽略数据的分层结构，认为所有数据都来自一个更大的总体(不区分站点)，只需要用一个回归方程来描述自变量与因变量的关系。

data:

\[ Y_i|\beta_0,\beta_1,\sigma~~\overset{ind}{\sim}~~N(\mu_i,\sigma^2)~~with~~\mu_i=\beta_0+\beta_1X_i \]

priors:

\[\begin{split} \beta_0~~\sim~~N(0,50^2)\\ \beta_1~~\sim~~N(0,5^2)\\ \sigma~~\sim~~Exp(1) \end{split}\]

  • 其中，\(Y_i\)是第i个被试的自我控制分数

  • \(X_i\)是第i个被试的压力得分

  • \(\beta_0和\beta_1\)是回归系数，\(\sigma\)是残差的标准差

  • \(\beta_1\)代表了压力与自我控制之间的关系

alt text

# 导入 pymc 模型包，和 arviz 等分析工具 
import pymc as pm
import arviz as az
import seaborn as sns
import scipy.stats as st
import numpy as np
import matplotlib.pyplot as plt
import xarray as xr
import pandas as pd
import ipywidgets
import bambi as bmb

# 忽略不必要的警告
import warnings
warnings.filterwarnings("ignore")

# 通过 pd.read_csv 加载数据 Data_Sum_HPP_Multi_Site_Share.csv
try:
  df_raw = pd.read_csv('/home/mw/input/bayes3797/Data_Sum_HPP_Multi_Site_Share.csv')
except:
  df_raw = pd.read_csv('data/Data_Sum_HPP_Multi_Site_Share.csv')

# 选取所需站点
first5_site = ['Southampton','Portugal','Kassel','Tsinghua','UCSB']
df_first5 = df_raw.query("Site in @first5_site")
# 生成站点索引
df_first5["site_idx"] = pd.factorize(df_first5.Site)[0]
# 生成被试数索引
df_first5["obs_id"] = range(len(df_first5))
# 将站点、被试id设置为索引
df_first5.set_index(['Site','obs_id'],inplace=True,drop=False)
df_first5

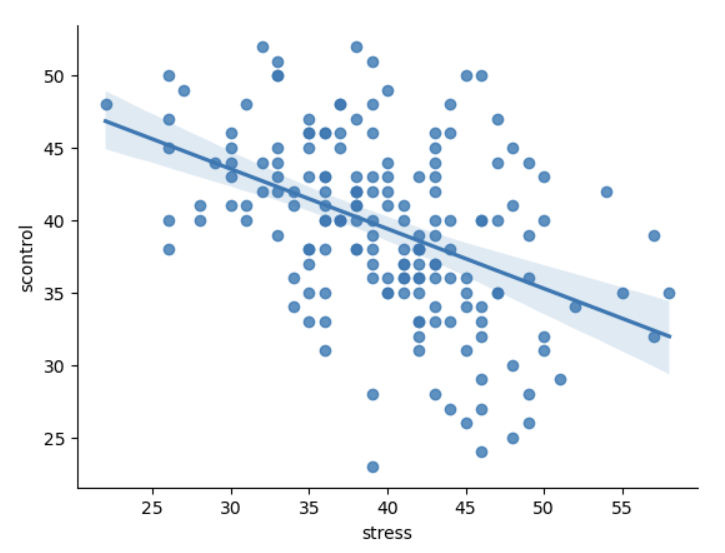
在处理数据之前，我们先按照完全池化的方式进行可视化，即不区分站点，把所有被试当成一个群体。

# 通过完全池化的方式可视化数据
sns.lmplot(df_first5,
           x="stress",
           y="scontrol",
           height=4, aspect=1.5)

alt text

模型定义与采样

data:

\[ Y_i|\beta_0,\beta_1,\sigma~~\overset{ind}{\sim}~~N(\mu_i,\sigma^2)~~with~~\mu_i=\beta_0+\beta_1X_i \]

priors:

\[\begin{split} \beta_0~~\sim~~N(0,50^2)\\ \beta_1~~\sim~~N(0,5^2)\\ \sigma~~\sim~~Exp(1) \end{split}\]
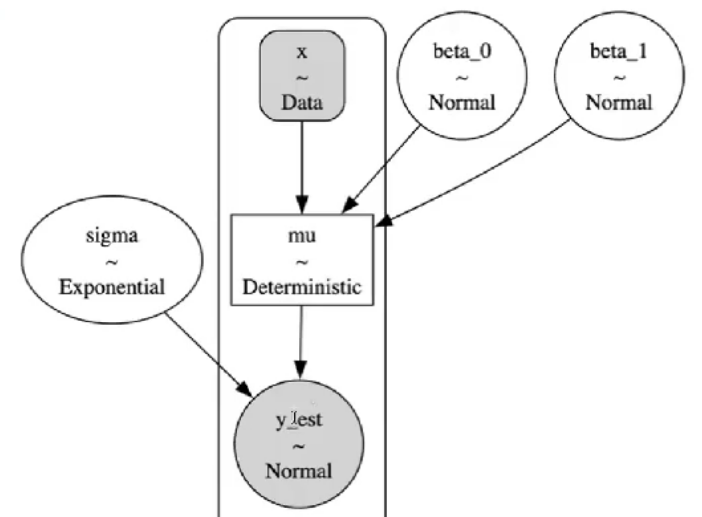
# 定义坐标映射
coords = {"obs_id": df_first5.obs_id}

with pm.Model(coords=coords) as complete_pooled_model:

    beta_0 = pm.Normal("beta_0", mu=0, sigma=50)                #定义beta_0          
    beta_1 = pm.Normal("beta_1", mu=0, sigma=5)                 #定义beta_1
    sigma = pm.Exponential("sigma", 1)                          #定义sigma

    x = pm.MutableData("x", df_first5.stress, dims="obs_id")    #x是自变量压力水平

    mu = pm.Deterministic("mu",beta_0 + beta_1 * x, 
                          dims="obs_id")                        #定义mu，讲自变量与先验结合

    likelihood = pm.Normal("y_est", mu=mu, sigma=sigma, observed=df_first5.scontrol,
                           dims="obs_id")                       #定义似然：预测值y符合N(mu, sigma)分布
                                                                #通过 observed 传入实际数据y 自我控制水平
    complete_trace = pm.sample(random_seed=84735)

pm.model_to_graphviz(complete_pooled_model)

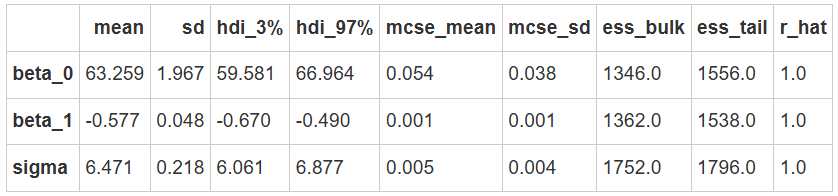
alt text

后验参数估计：

结果显示：

\[\begin{split} \mu_i=\beta_0+\beta_1X_i\\ \beta_0=63.17\\ \beta_1=-0.58 \end{split}\]

  • \(\beta_1=-0.58\)表明，在给定站点的情况下，自我控制水平与压力水平之间存在负相关关系。并且，压力分数每增加1分，自我控制水平平均下降0.58分。

az.summary(complete_trace,
           var_names=["~mu"],
           filter_vars="like")

alt text

后验预测回归线

#提取不同站点数据对应的索引并储存，便于后续将后验预测数据按照站点进行提取
def get_group_index(data):
    group_index = {}
    for i, group in enumerate(data["Site"].unique()):
        group_index[group] = xr.DataArray(data.query(f"Site == '{group}'"))["obs_id"].values
    return group_index

#定义函数，绘制不同站点下的后验预测回归线
def plot_regression(data, trace, group_index):
    # 定义画布，根据站点数量定义画布的列数
    fig, ax = plt.subplots(1,len(data["Site"].unique()), 
                       sharex=True,
                       sharey=True,
                       figsize=(15,5))
    
    # 根据站点数来分别绘图
    # 需要的数据有原始数据，每一个因变量的后验预测均值
    # 这些数据都储存在后验参数采样结果中，也就是这里所用的trace
    for i, group in enumerate(data["Site"].unique()):
        #绘制真实数据的散点图
        x = trace.constant_data.x.sel(obs_id = group_index[f"{group}"])
        y = trace.observed_data.y_est.sel(obs_id = group_index[f"{group}"])
        mu = trace.posterior.mu.sel(obs_id = group_index[f"{group}"])
        ax[i].scatter(x, y,
                color=f"C{i}",
                alpha=0.5)
        #绘制回归线
        ax[i].plot(x, mu.stack(sample=("chain","draw")).mean(dim="sample"),
                color=f"C{i}",
                alpha=0.5)
        #绘制预测值95%HDI
        az.plot_hdi(
            x, mu,
            hdi_prob=0.95,
            fill_kwargs={"alpha": 0.25, "linewidth": 0},
            color=f"C{i}",
            ax=ax[i])
    # 生成横坐标名称
    fig.text(0.5, 0, 'Stress', ha='center', va='center', fontsize=12)
    # 生成纵坐标名称
    fig.text(0.08, 0.5, 'Self control', ha='center', va='center', rotation='vertical', fontsize=12)
    # 生成标题
    plt.suptitle("Posterior regression models", fontsize=15)
        
    sns.despine()

# 获取每个站点数据的索引
first5_index = get_group_index(data=df_first5)
# 进行可视化
plot_regression(data=df_first5,
                trace=complete_trace,
                group_index=first5_index)

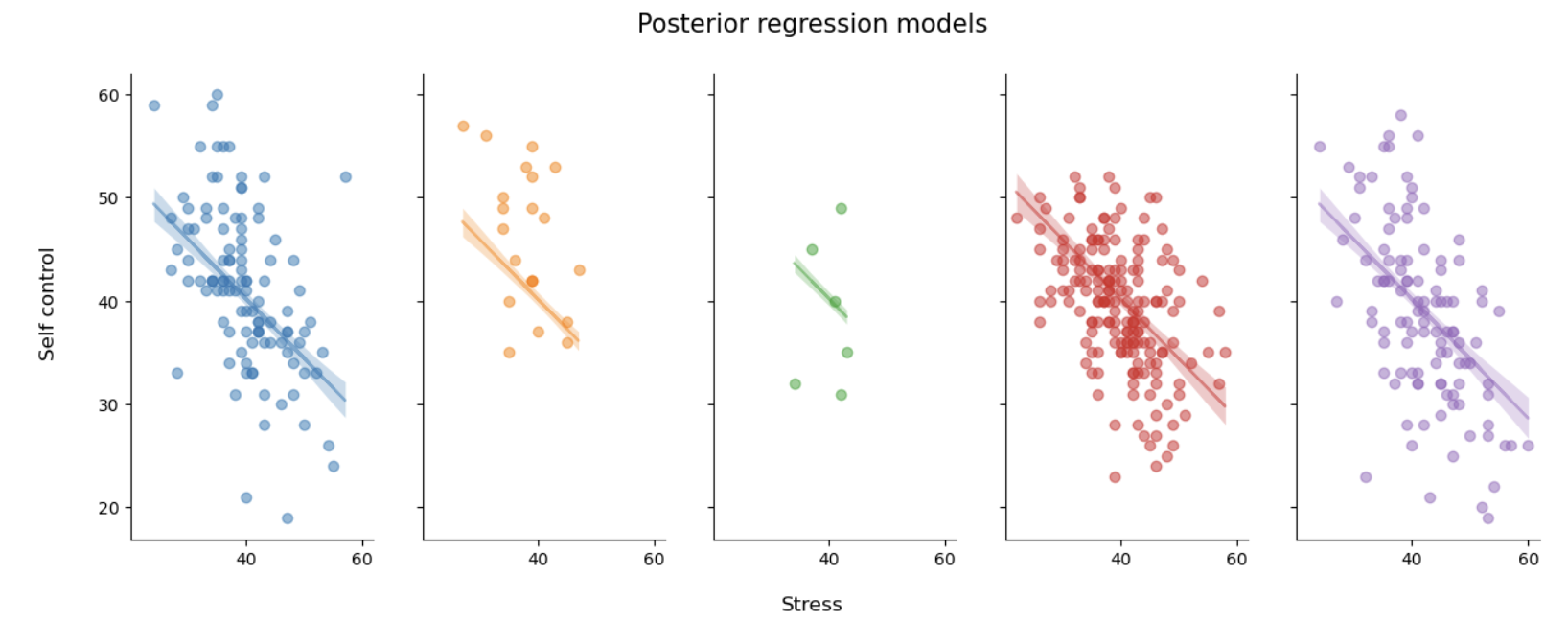
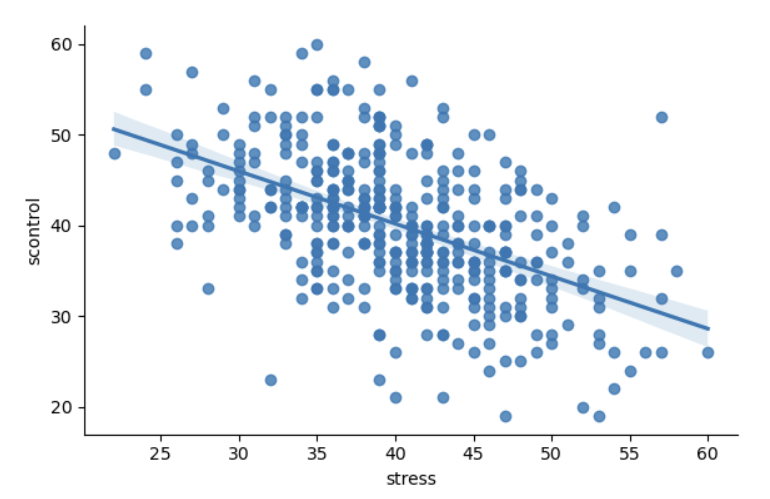
alt text

  • 通过上面的图可以直观地看出，不同站点回归线的斜率和截距几乎是一致的。

  • 完全池化模型假设，所有站点中自我控制分数一致，并且压力的影响也一致。

Contents