Part 4: 频率学派与贝叶斯学派的对比#
最近的一篇综述讨论了贝叶斯方法在临床研究设计和分析中的应用,同时比较了贝叶斯与频率主义方法之间的哲学和方法论差异。

论文中展示的一个例子是一项用于治疗严重急性呼吸窘迫综合征(ARDS)的体外膜肺氧合法(ECMO)试验,研究体外膜肺氧合法(ECMO)对严重急性呼吸窘迫综合征(ARDS)的效果。该试验的结果引发了频率学派和贝叶斯学派在同一数据下得出不同结论的讨论。
频率学派 试验原本计划招募331名患者,但因中期分析未能证明ECMO治疗具有显著益处,最终只招募了249名患者。结果显示,干预组的死亡率为35%,对照组为46%,表面上看治疗效果显著。然而,基于频率学派的统计分析,\( P \)值为0.09,并未达到通常的显著性水平(\( p<0.05 \))。
因此研究者得出结论:试验未能提供充分证据证明早期ECMO可以显著降低死亡率。
贝叶斯学派
通过使用不同的先验分布时,\( H_1 \)(ECMO可以有效降低干预组死亡率)成立的后验概率在88%至99%之间。 这意味着,贝叶斯方法提供了强有力的证据支持ECMO的效果,甚至有学者建议,ECMO方法应被认为是一种有效的治疗手段。
频率学派如何看待这个世界?#
在对比频率学派与贝叶斯学派的差异之前,让我们首先回顾一下频率学派是如何看待这个世界的。
值得注意的是:
1、固定的假设:频率学派认为假设(通常是零假设)是一个固定的命题。例如,在试验中,频率学派的零假设是“ECMO对死亡率没有显著影响”。
2、数据的随机性:在频率学派的框架下,数据被视为随机变量。通过对这些数据进行分析,频率学派关注在假设为真的前提下,观测到当前数据或更极端数据的概率,即\( p \)值。
3、无限重复实验的假设:频率学派的推断依赖于假设实验可以无限重复进行,进而通过计算在这些重复实验中得到观测数据的频率来推断真相。因此,置信区间也是基于多次实验的频率分布。
4、拒绝或接受零假设:通过计算\( p \)值,频率学派根据预设的显著性水平(通常为0.05)决定是否拒绝零假设。
最后,频率学派如何推断出两个总体之间的差异?
1、频率学派通过零假设的显著性检验(Null hypothesis significant test, NHST)来判断显著性。通过计算置信区间(confidence interval)和\( p \)值来帮助推断过程。
2、在该临床试验中,通过\( p \)值(如,0.09)和置信区间来推断两个总体之间的差异。
贝叶斯学派如何看待这个世界?#
与频率学派不同,贝叶斯学派认为:概率是对不确定性的主观度量。
贝叶斯学派的核心思想包括:
1、先验概率:贝叶斯学派从研究者对某个假设的初始信念(即先验概率)出发。这一信念可以基于以往研究、专家意见或临床经验。
2、更新信念:当新数据(如试验结果)出现时,贝叶斯定理提供了一个框架,将先验概率与新证据(通过似然函数表示)结合,生成后验概率。后验概率代表更新后的信念,即在观察到新数据后,某假设为真的概率。
3、后验分布与可信区间(credible intervals):通过后验概率,贝叶斯方法能够直接评估一个假设为真的可能性。例如,贝叶斯分析可以直接得出H1成立的后验概率(如88%)。可信区间的概念也更具直观性,它表示在现有数据和先验信息下,某参数位于该区间内的概率。
两个学派的差异对比:频率学派 vs 贝叶斯学派#
频率学派 |
贝叶斯学派 |
|---|---|
概率定义:概率是事件在无限重复试验中的频率 |
概率定义:概率是对假设的信念度量 |
假设:假设是固定的,数据是随机的 |
假设:假设是随机的,数据是固定的 |
推断方式:基于假设检验,通过\( p \)值判断是否拒绝零假设 |
推断方式:通过更新先验与新数据计算后验概率 |
置信区间:在重复试验中,95%的区间包含真实参数 |
可信区间:给出某参数位于区间内的概率(如95%可信度) |
\( p \)值:衡量在零假设下,观测数据或更极端数据的概率 |
后验概率:给出假设为真的更新概率 |
数据独立性:推断只基于当前试验数据,不考虑先验信息 |
先验信息:结合历史数据或专家意见,用于更新推断 |
实验重复性假设:推断基于实验的假想重复性 |
逐步积累信息:通过结合新数据不断更新和完善假设 |
适应性:实验设计固定,不能在中途更新或调整 |
适应性:可以灵活调整试验设计和决策,如自适应试验 |
来源:
Goligher, E. C., Heath, A., & Harhay, M. O. (2024). Bayesian statistics for clinical research. The Lancet, 404(10457), 1067-1076.
贝叶斯的主观性
任何统计分析方法都不可能完全客观,因此主观性是一个相对概念:
1、贝叶斯学派的主观性通过先验的设定来体现,透明,不易让人产生误解
2、频率学派的主观性暗含在各种前提预设中,比如方差分析中的方差齐性和正态性,这种看似‘客观的’预设,一方面难以满足,一方面也是一种主观的设定。
3、更为宏观的来说,样本的抽取,数据清理方式的选择,分析方法的选择,\( p \)值的设定,这些都存在主观性。(例如,用作统计推断的临界P值0.05的设定是早年统计学家们的一个比较随意的论断,但后来就成为各个领域的普遍标准)因此,频率学派并没有想象的那么‘客观’。
4、主观不一定是坏事:通过量化方法将个体的经验和专家知识整合到数据分析之中。
重复抽样的不同作用
频率学派
1、统计推断依赖于参数的抽样分布,即只要无限(long-run)的进行抽样,样本分布的参数就会有某种分布形式。
2、零假设检验(Null Hypothesis Significance Testing,NHST)中的\( p \)值和置信区间的解读均依赖于“无限次抽样”的预设。(但实际上来看,无限次抽样是无法实现的,例如很多历史事件可能只会发生一次)
3、实际操作中,我们往往只会收集一次数据,并不会反复的进行抽样;有些情境中,预设“无限次重复抽样并不合理
贝叶斯学派
1、假定参数本身是分布,不确定性一起存在于推断之中
2、直接根据数据对先验信念进行更新
置信区间(confidence intervals) vs 可信区间(credible intervals)
——No free lunch: 各有优势和缺陷
感兴趣的可以在R psychologist网站进行深入了解:https://rpsychologist.com/
不同的先验和似然会产生不同的后验分布
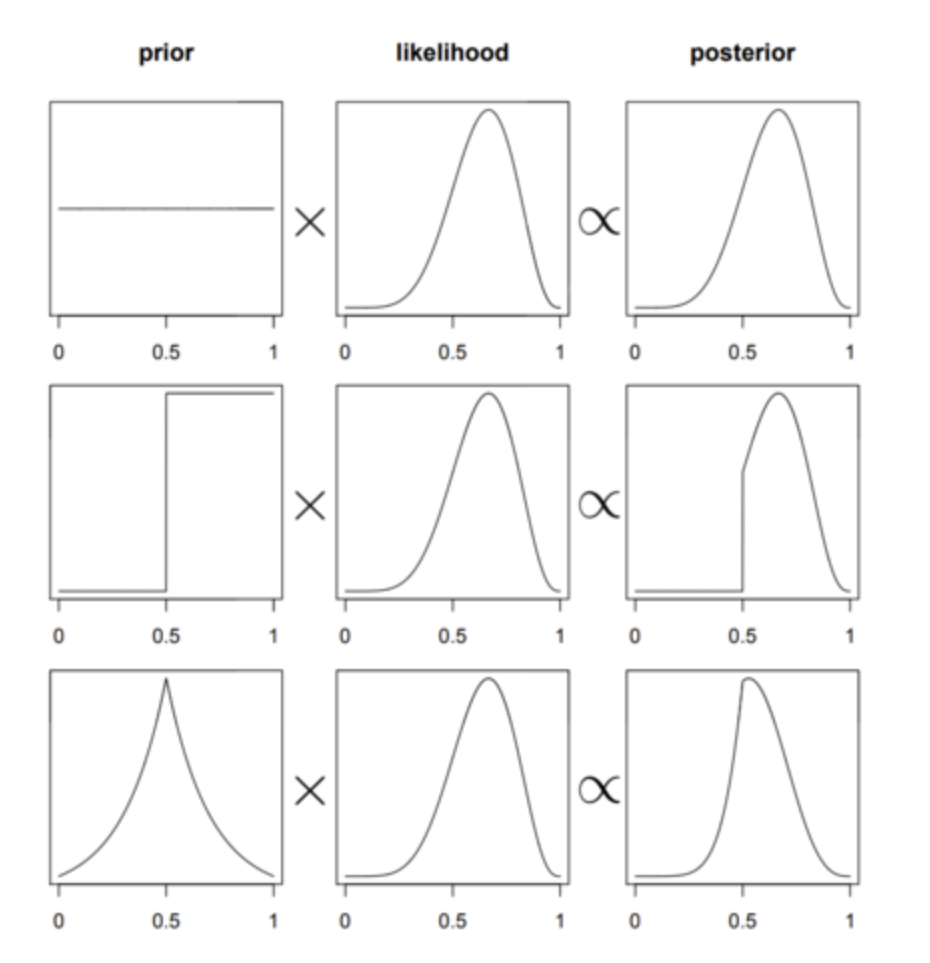
从上面的图我们可以看出,中间这一列都是相同的likelihood,但由于先验(左列)不同,后验(右列)也会发生变化。因此,如何选择一个合理的先验是非常重要的,后面课程我们将详细介绍先验如何选择。
NHST的”弱项”
1、无法直接对零假设(null hypothesis)进行支持,即如果两个总体没有显著差异,他们的相似程度有多少? (许岳培等, 2023, 应用心理学(04), 369-384)
2、一次性只能对比两个总体的假设进行比较
3、控制假阳性是一个棘手的问题
