Logistic Regression#
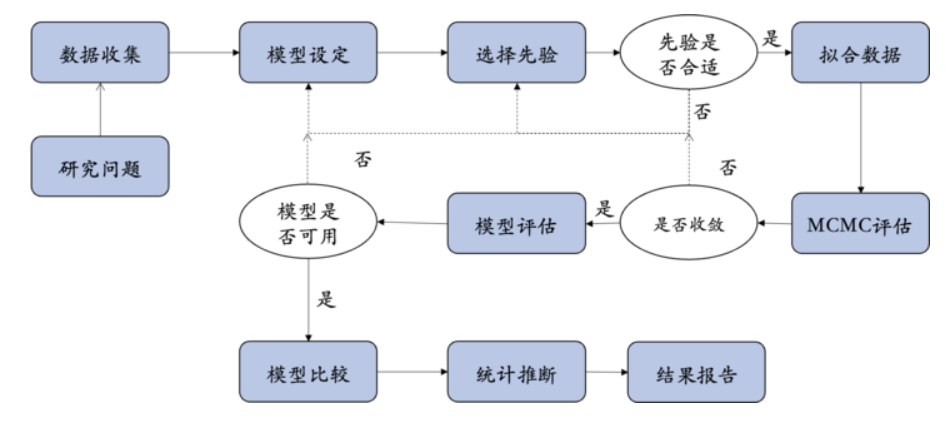
回顾:贝叶斯视角下的回归模型#
在贝叶斯统计框架下,回归模型的构建与检验方法与传统频率学派有所不同。
在贝叶斯回归中,模型的参数被视为随机变量,通过数据来更新其概率分布。
贝叶斯方法通过对参数的后验分布进行推断,从而评估模型的适应性与显著性。
这种方法使得我们不仅能得到参数的点估计,还能获得关于这些参数的不确定性的信息。
在之前的课程中,我们以自我优势匹配范式为例,建立了一个简单的线性回归模型:
在这个模型中,反应时(RT)是一个连续的因变量。
然而,在许多心理学研究中,另一个最常见的因变量就是反应是否正确,这通常是一个二分变量(正确 / 错误)。
🤔思考:当因变量是二分变量时,传统的线性回归模型是否仍然适用呢?
以随机点运动任务为例:贝叶斯逻辑回归#
接下来,我们以之前介绍过的随机点运动任务(Random Motion Dot Task)为例,来理解贝叶斯逻辑回归模型的应用。
在这个实验中,参与者观察屏幕上随机运动的点,这些点的运动方向具有一定的一致性(即大部分点朝某一方向移动)。
参与者的任务是判断这些点的主要移动方向(例如,向左还是向右)。
实验设计可以控制点的运动一致性(如10%或40%),从而影响参与者作出正确决策的难度。
和之前的内容不同,本次课我们将研究点的运动一致性与判断是否正确之间的关系:
1.自变量:点的运动一致性(10%一致性,40%一致性)
2.因变量:判断是否正确(即被试是否准确判断了点的主要运动方向,1代表反应正确,0代表反应错误)
我们本次将研究点的运动一致性与判断是否正确之间的关系:
1.自变量:点的运动一致性(10%一致性和40%一致性)
2.因变量:判断是否正确即被试是否准确判断了点的主要运动方向,1代表反应正确,0代表反应错误)
以Evans et al.(2020, Exp. 1) 的数据为例进行探索。
Evans, N. J., Hawkins, G. E., & Brown, S. D. (2020). The role of passing time in decision-making. Journal of Experimental Psychology: Learning, Memory, and Cognition, 46(2), 316–326. https://doi.org/10.1037/xlm0000725
首先,我们导入数据并查看其分布情况:
# 导入 pymc 模型包,和 arviz 等分析工具
import pymc as pm
import arviz as az
import seaborn as sns
import scipy.stats as st
import numpy as np
import matplotlib.pyplot as plt
import xarray as xr
import pandas as pd
import ipywidgets
# 忽略不必要的警告
import warnings
warnings.filterwarnings("ignore")
# 使用 pandas 导入示例数据
try:
df = pd.read_csv("/home/mw/input/bayes3797/evans2020JExpPsycholLearn_exp1_full_data.csv")
except:
df = pd.read_csv('data/evans2020JExpPsycholLearn_exp1_full_data.csv')
# 筛选编号为 31727 的数据,并且筛选出两个不同的 percentCoherence
df_clean = df[(df['subject'] == 31727) & (df['percentCoherence'].isin([10, 40]))]
df_clean = df_clean[["subject", "percentCoherence", "correct"]]
df_clean
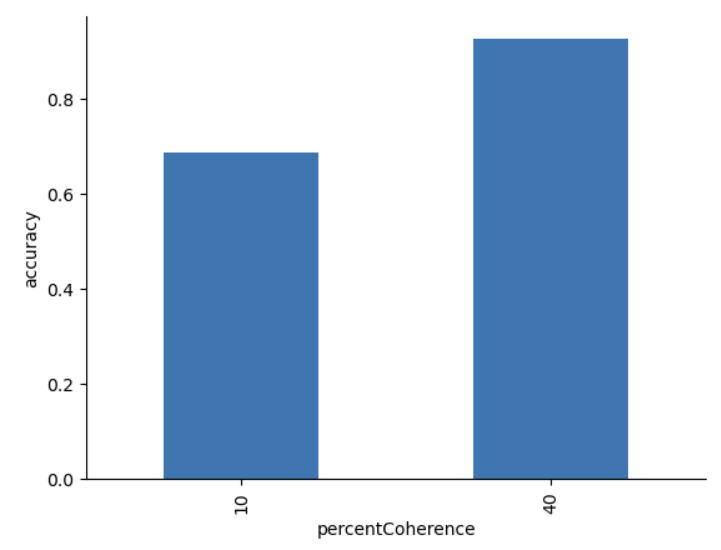
df_clean.groupby("percentCoherence").correct.mean()
output: percentCoherence 10 0.686047 40 0.926316 Name: correct, dtype: float64
# 因变量分布
ax = df_clean.groupby("percentCoherence").correct.mean().plot.bar()
ax.set_ylabel("accuracy")
sns.despine()
plt.show()
通过散点图,我们可以直观地观察到数据中不同变量的分布情况:
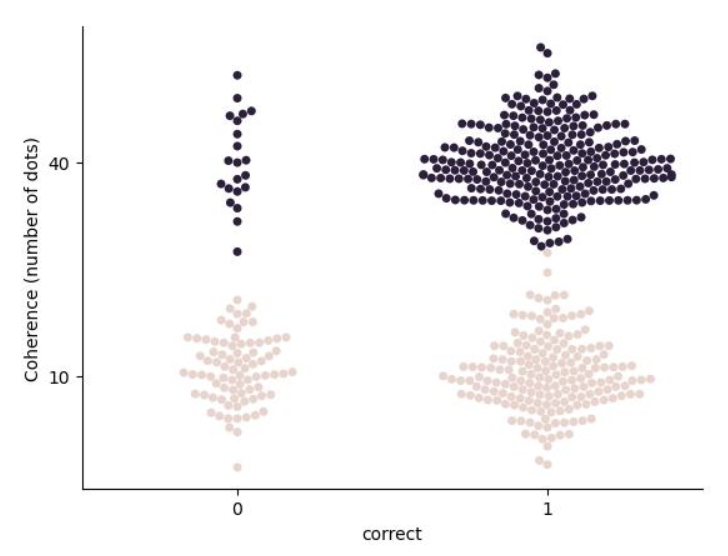
在示例数据中中,
因变量“correct”是一个二分类变量,表示被试是否获得正确反应。
我们考虑的自变量“percentCoherence”可以是连续变量,表示被试的刺激强度 (percentCoherence 或 motion strength)。
我们感觉兴趣的是“correct”与“percentCoherence”之间的关系。
问题:我们能否使用线性回归分析正确率数据?#
在我们传统的认知实验研究的数据分析中,一般最简单的方法就是使用t检验或者方差分析(线性回归模型的特例)对正确率进行分析,这就是我们常说的“遵循领域内的传统”。
然而,这样处理的前提是将正确率作为一个连续数据看待,并采用线性回归模型对它进行分析,这实际上严格来说是存在问题的。
1、我们能否对每一个试次的数据进行分析?
如果只是将所有试次的数据求一个平均的话,实际上并没有体现出数据量的大小所带来的影响(丢失了这一部分的信息),例如在之前贝叶斯基本原理的课程中所介绍的“数据不一样,后验更新也会不同”。
2、如果我们使用线性回归模型对正确率进行分析,会存在什么问题?
首先,我们需要建立起因变量y(取值为0或1)和自变量x的线性关系:
存在的问题:
线性回归模型中的因变量y服从一个正态分布,它的理论取值应当是负无穷到正无穷,但是我们每个试次的取值只能为0或1,并不满足y的理论取值。
3、如果对二分变量的模型参数进行回归分析,会存在什么问题?
正确反应的概率可以看作是一个伯努利分布,即\(Y_i|\pi_i \sim Bern(\pi_i)\),其中\(\pi_i\)是在刺激强度(运动一致性)\(x_i\)下被试获得正确反应的概率。
曲线上的每一个点都服从伯努利分布\(Y_i|\pi_i \sim Bern(\pi_i)\)。
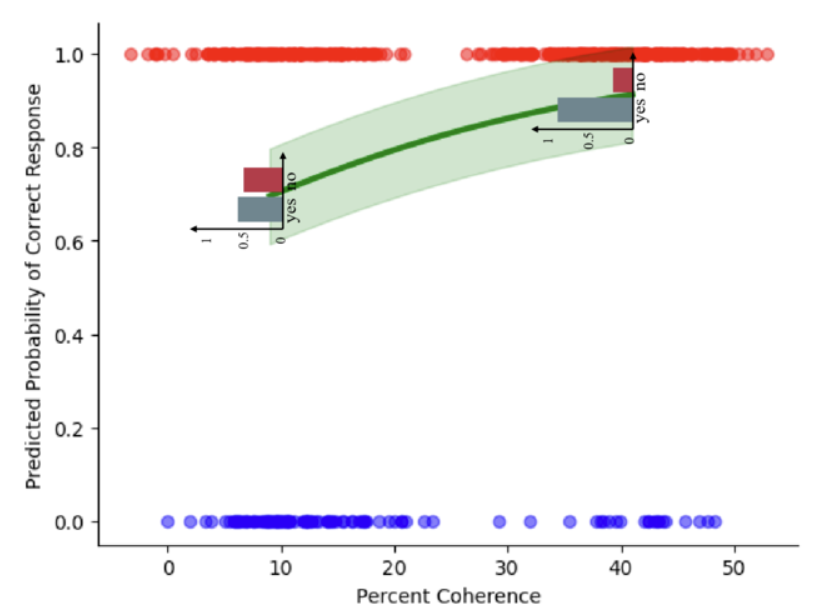
存在的问题:
我们在做后验预测时仍然可能存在问题,因为仍然是根据正态分布对\(\pi\)进行后验预测,此时还是会很容易出现0-1区间以外的取值。
至此,我们引入一个新概念———发生比(odds)
Probability & odds#
与概率不同,发生比(odds)描述的是事件发生概率与事件不发生概率之比,而概率描述的是事件发生的绝对可能性。
\(\pi\)为因变量Y发生的概率
举例:明天是否会下雨?
我们假设明天下雨发生的概率是\(\pi=2/3\),那么明天不下雨的概率为\(1-\pi=1/3\)
\(\pi\)的取值为(0,1),odds的取值为[0,+∞)
将发生比与1进行比较来衡量事件发生的不确定性:
1.当事件发生的概率\(\pi<0.5\)时,事件的发生比小于1
2.当事件发生的概率\(\pi=0.5\)时,事件的发生比等于1
3.当事件发生的概率\(\pi>0.5\)时,事件的发生比大于1
虽然我们将\(\pi\)的取值范围扩大到了[0, +∞),但仍然无法满足(-∞,+∞)的取值范围。
因此,我们还需要继续进行转换。
进一步对odds进行转换,让其在正负无穷上均有取值——log(odds)
log后,取值范围符合(-∞,+∞)。
总结起来:
在广义线性模型中,我们需要连接函数(link function)g(⋅),使得参数\(g(\pi_i)\)可以被表示为自变量\(X_{i1}\)的线性组合。
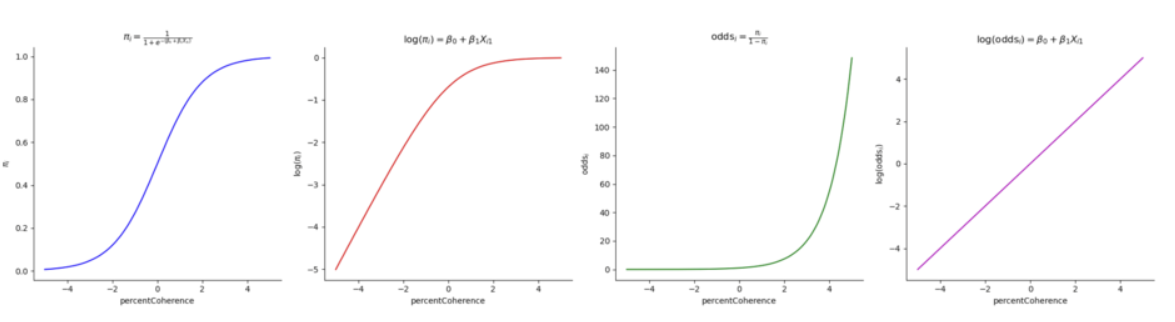
总的来说,对于其他的数据类型,我们也可以先找到符合其特点的统计分布以及这种分布的参数,然后对它进行相应的转换并符合我们回归模型的特征,最后基于连接函数建立起自变量和因变量之间的线性关系。
广义线性模型(Generalized Linear Model, GLM)#
对线性回归模型的推广
在因变量不满足线性模型的预设条件时,仍然使用线性模型的思路。
核心在于通过连接函数对因变量进行变换,使其满足线性模型的条件。
对二分变量的广义线性模型称为逻辑回归,还有大量适用于其他数据的广义线性模型,本质上是一致的。
回归系数的解释是难点,需要领域特殊的知识。最关键的在于,x每变化一个单位y是如何变化的,以及所对应的beta值如果显著,它所对应的特定含义是什么。
公式中各参数的意义
\(\beta_0\)是截距项,也称为常数项,它表示当所有自变量(\(X_1,X_2,...,X_p\))都为0时,log(odds)的基线值。换句话说,\(\beta_0\)表示模型在无任何预测变量影响时的log(odds)。
\(\beta_1,\beta_2,...,\beta_p\)是回归系数,分别表示每个预测变量(\(X_1,X_2,...,X_p\))对log(odds)的影响。即,每个\(\beta_i\)表示对应自变量\(X_i\)增加一个单位时,log(odds)变化的大小。
Gelman, A., & Hill, J. (2006). Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge: Cambridge University Press.
也可以写成:
\(\beta_0\)
当(\(X_1,X_2,...,X_p)=0时,odds=e^{\beta_0},即e^{\beta_0}\)表示当所有自变量为0时,事件的发生比
\(\beta_1\)
\(\beta_1=log(odds_{x+1})-log(odds_x) \rightarrow e^{\beta_1}=\frac{odds_{x+1}}{odds_x}\)
当其他自变量保持不变时,\(X_1\)每增加一个单位(从\(X \rightarrow X+1\)),\(e^{\beta_1}\)表示事件发生比的倍数变化。
计算
补充知识:更多可用的分布
分布类型 |
描述概率 |
描述发生比 |
适用情况说明 |
|---|---|---|---|
二项分布 |
是 |
否 |
描述n次独立伯努利试验中成功次数的概率分布 |
贝塔分布 |
是 |
是 |
描述伯努利试验中成功概率的先验分布,也可以用来描述发生比 |
对数正态分布 |
否 |
是 |
描述正态分布变量取对数后的分布,常用于描述正比于发生比的数据 |
泊松分布 |
是 |
否 |
描述在固定时间或空间内发生某事件的次数的概率分布 |
伽马分布 |
否 |
是 |
描述等待时间的分布,常用于作为泊松分布中事件发生率的先验分布,因此可以用来描述发生比 |
负二项分布 |
是 |
否 |
描述在获得r次成功之前经历n次试验的概率分布,适用于成功概率不固定的情况 |
多项分布 |
是 |
否 |
描述多项式试验中各种结果次数的概率分布 |
Dirichlet分布 |
是 |
是 |
描述多项分布中各种结果概率的先验分布,也可以用来描述发生比 |
贝叶斯广义线性模型的定义与代码实现#
现在,我们已经了解了逻辑回归模型的基本结构,我们可以开始定义模型:
我们需要确定变量类型和分布。
需要根据连接函数(link function)来设置转化参数。
并且为转化后的参数设置先验分布。
首先,为转换后的参数设置先验分布:
注意:这里的参数先验是经过 logit 转后后的值,而不是概率。 因此,我们需要根据先验预测检验来确定先验分布参数设置是否正确。
# 数据准备
Treatment_Coding,_ = df_clean['percentCoherence'].factorize() # 适用 treatment 编码
y = df_clean['correct'].values # 目标变量
# 模型构建
with pm.Model() as log_model1:
# 添加数据,方便后续绘图
pm.MutableData("percentCoherence", df_clean['percentCoherence'])
# 设置先验
# 通常我们会为截距和系数设置正态分布的先验
intercept = pm.Normal('beta_0', mu=0, sigma=10)
coefficient = pm.Normal('beta_1', mu=0, sigma=10)
# 线性预测
linear_predictor = intercept + coefficient * Treatment_Coding
# 似然函数
# 使用逻辑函数将线性预测转换为概率
# 方法一:自行进行 logit link 转换
pi = pm.Deterministic('pi', pm.math.invlogit(linear_predictor))
likelihood = pm.Bernoulli('likelihood', p=pi, observed=y)
# 方法二:直接使用 logit_p 进行转换
# likelihood = pm.Bernoulli('likelihood', logit_p=linear_predictor, observed=y)
注意代码中使用了pm.math.invlogit函数,它相当于计算了 Logistic sigmoid function,即\(1/(1+e^{-\mu})\)
为了方便我们自行进行转化,我们可以自行定义这个函数,如下:
def inv_logit(x):
return np.exp(x) / (1 + np.exp(x))
先验预测检验
使用pm.sample_prior_predictive进行先验预测检验,来查看由当前先验组合生成的\(\pi\)是否都在0至1的范围内
log1_prior = pm.sample_prior_predictive(samples=50,
model=log_model1,
random_seed=84735)
log1_prior
在模型定义中我们已经对pi进行定义,因此
pm.sample_prior_predictive就会自动生成对pi的预测该预测储存在prior中
我们设置抽样数为50,这体现在维度draw中
结合循环,使用
sns.lineplot绘制出每个回避分数对应的π值并连接成光滑的曲线
#对于一次抽样,可以绘制出一条曲线,结合循环绘制出50条曲线
for i in range(log1_prior.prior.dims["draw"]):
sns.lineplot(x = log1_prior.constant_data["percentCoherence"],
y = log1_prior.prior["pi"].stack(sample=("chain", "draw"))[:,i], c="grey" )
#设置x、y轴标题和总标题
plt.xlabel("percentCoherence",
fontsize=12)
plt.ylabel("probability of correct",
fontsize=12)
plt.suptitle("Relationships between percentCoherence and the probability of correct",
fontsize=14)
sns.despine()
plt.show()
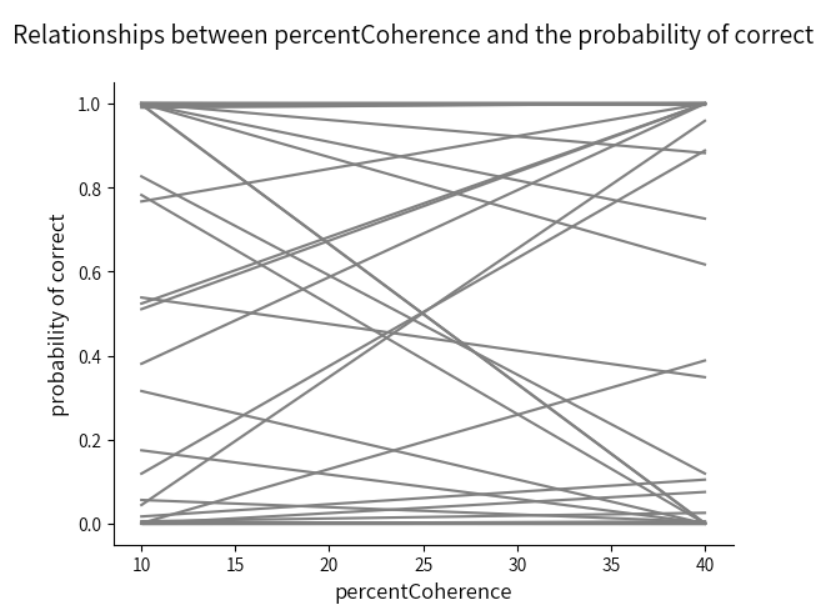
我们可以看到,在一致性10%和40%这两种条件下,所对应的正确率基本上都在0-1范围之间,因此是可以接受。当然,也可以对prior进行优化,但需要比较谨慎地去考虑。
注意:prior的优化需要很谨慎地进行
在贝叶斯中,如果为了得到一个特定的后验去把先验改的特别精确,最后导致数据的作用很小,这实际上类似于我们传统零假设检验中的“P hacking”,也就是为了让P值变小做各种各样数据的优化。因此,为了避免这种嫌疑,先验优化是需要非常谨慎的。
MCMC采样 & 模型诊断
#===========================
# 注意!!!以下代码可能需要运行35s~1分钟左右
#===========================
with log_model1:
# 模型编译和采样
log_model1_trace = pm.sample(draws=5000,
tune=1000,
chains=4,
discard_tuned_samples=True,
random_seed=84735)
az.plot_trace(log_model1_trace,
var_names=["beta_0","beta_1"],
figsize=(7, 6),
compact=False)
plt.show()
后验参数解释
fitted_parameters = az.summary(log_model1_trace, var_names=["beta_0","beta_1"])
fitted_parameters
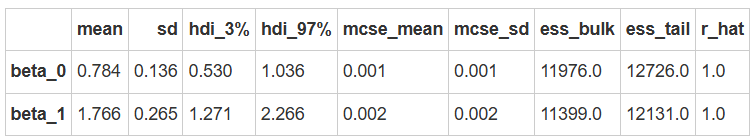
为了将发生比转换为概率,我们需要计算适用逆运算,如下:
def inv_logit(log_odds):
return np.exp(log_odds) / (1 + np.exp(log_odds))
p_coh10 = inv_logit( fitted_parameters.loc["beta_0", "mean"])
p_coh40 = inv_logit(
fitted_parameters.loc["beta_1", "mean"] + \
fitted_parameters.loc["beta_1", "mean"]
)
print(f"p(coherence=10) = {p_coh10:.3f}", f"p(coherence=40) = {p_coh40:.3f}")
p(coherence=10) = 0.687 p(coherence=40) = 0.972
# 通过 inv_logit 将 beta 参数进行转换
az.plot_posterior(log_model1_trace, var_names=["beta_0"], transform = inv_logit)
plt.show()
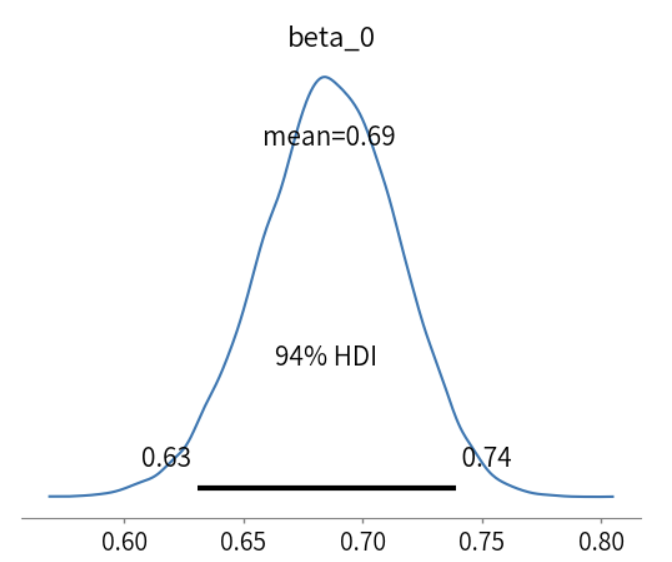
结果显示:
\(\beta_0=0.786,那么e^{\beta_0}=2.195,X_{i1}=0时,则事件发生的odds为e^{\beta_0}为2.195\)。
\(\beta_1=1.765,e^{\beta_1}=5.859,X_{i1}每增加1个单位,odds将增加e^{\beta_1}的5.859倍\)。
然而,\(\beta_1\)的4%HDI包括0,说明点的一致性方向概率不能有效预测判断是否正确的概率。
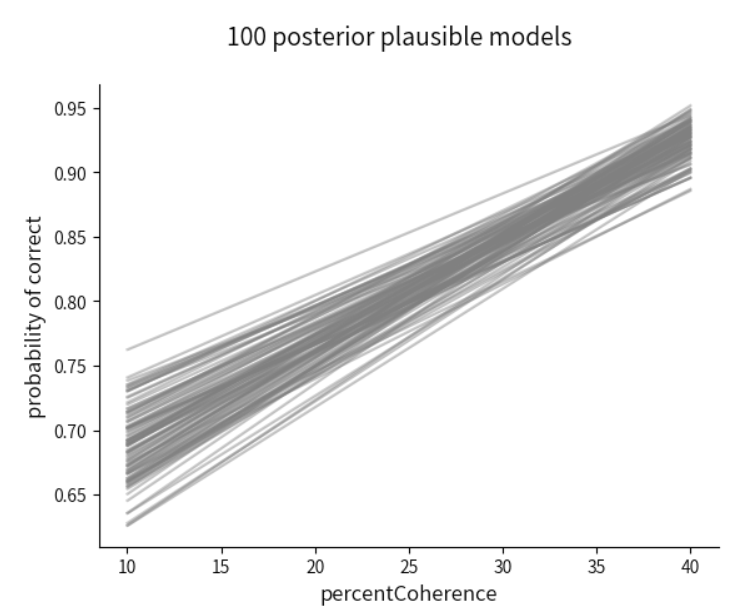
后验回归模型
绘制后验预测回归线
和先验预测模型类似的,通过MCMC采样,也同样生成了对π的估计,储存在posterior中。
有4条马尔科夫链,每条链上的采样数为2000,所以对于每一个x,都生成了20000个预测值π,这样就对应着20000条后验预测回归线
这里我们只需要画出100条即可
log_model1_trace
#对于一次抽样,可以绘制出一条曲线,结合循环绘制出50条曲线
ys = log_model1_trace.posterior["pi"].stack(sample=("chain", "draw"))
for i in range(100):
sns.lineplot(x = log_model1_trace.constant_data["percentCoherence"],
y = ys[:,i],
c="grey",
alpha=0.4)
#设置x、y轴标题和总标题
plt.xlabel("percentCoherence",
fontsize=12)
plt.ylabel("probability of correct",
fontsize=12)
plt.suptitle("100 posterior plausible models",
fontsize=14)
sns.despine()
plt.show()
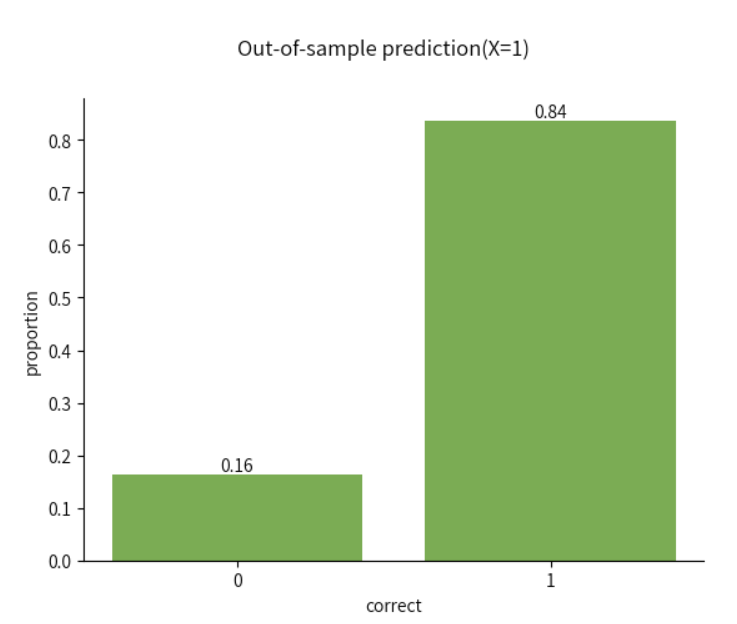
对新数据进行预测&分类
除了对当前数据结果做出解释,也可以使用当前的参数预测值,对新数据做出预测
现在假设有一批新数据,那么被试在“percentCoherence”为 40的情况下,对新数据进行正确判断的概率是多少?
即当\(X_i=40\)时,对新数据进行预测和分类
由于例子中的自变量使用了treatment coding的编码方式,所以\(X_i=40\)对应为\(X_i=1\)
odds = log_model1_trace.posterior["beta_0"]+ log_model1_trace.posterior["beta_1"] * 1
pi = inv_logit(odds)
Y_hat = np.random.binomial(n=1, p=pi)[0]
# 统计其中0和1的个数,并除以总数,得到0和1对应的比例值
y_pred_freq = np.bincount(Y_hat)/len(Y_hat)
# 绘制柱状图
bars = plt.bar([0, 1], y_pred_freq, color="#70AD47")
# 用于在柱状图上标明比例值
for bar, freq in zip(bars, y_pred_freq):
plt.text(bar.get_x() + bar.get_width() / 2, bar.get_height(), f"{freq:.2f}", ha='center', va='bottom')
#对刻度、标题、坐标轴标题进行设置
plt.xticks([0, 1])
plt.suptitle("Out-of-sample prediction(X=1)")
plt.xlabel("correct")
plt.ylabel("proportion")
sns.despine()
评估分类结果
我们可以使用混淆矩阵(confusion matrix)来对真实结果与预测结果进行比较和评估(0为阴性,1为阳性):
这种矩阵类似于我们的信号检测论、一类错误二类错误矩阵等等,虽然她们有不同的术语,但是基本原理是相同的。
a: 真阴性(True Negative,TN)表示被正确预测为负例的样本数
b: 假阳性(False Positive,FP)表示被错误预测为正例的样本数
c: 假阴性(False Negative,FN)表示被错误预测为负例的样本数
d: 真阳性(True Positive,TP)表示被正确预测为正例的样本数
\(\hat{Y}=0\) |
\(\hat{Y}=1\) |
|
|---|---|---|
\(Y=0\) |
a |
b |
\(Y=1\) |
c |
d |
在二分类问题中,准确性(Accuracy)、敏感性(Sensitivity)和特异性(Specificity)是常用的评估指标,可以通过在得到 a b c d 的数量之后进行计算:
准确性(accuracy) :准确性是指分类模型正确预测的样本数占总样本数的比例。
准确性衡量了模型总体的分类正确率,数值越高表示模型的整体性能越好。
敏感性(sensitivity) :敏感性也称为召回率(Recall),它是指在所有实际为正例的样本中,被正确预测为正例的比例。
敏感性衡量了模型对于正例的识别能力,数值越高表示模型对于正例的预测能力越好。
3.特异性(specificity) :特异性是指在所有实际为负例的样本中,被正确预测为负例的比例。
特异性衡量了模型对于负例的识别能力,数值越高表示模型对于负例的预测能力越好。
现在,我们来计算一下这三个指标:
ys = log_model1_trace.posterior["pi"].stack(sample=("chain", "draw"))
df_clean["pi"] = ys.mean(dim="sample").values
predictions = []
for i in df_clean["pi"]:
prediction = np.random.binomial(n=1, p=i)
predictions.append(prediction)
df_clean["prediction"] = predictions
df_clean
def calculate_contingency_table(df, y="correct", yhat="prediction"):
# 计算各种情况的数量
TN = ((df[y] == 0) & (df[yhat] == 0)).sum() # 真阴性
FP = ((df[y] == 0) & (df[yhat] == 1)).sum() # 假阳性
FN = ((df[y] == 1) & (df[yhat] == 0)).sum() # 假阴性
TP = ((df[y] == 1) & (df[yhat] == 1)).sum() # 真阳性
# 创建一个DataFrame来表示列联表
contingency_df = pd.DataFrame({
'$\\hat{Y} = 0$': [TN, FN],
'$\\hat{Y} = 1$': [FP, TP]
}, index=['$Y=0$', '$Y=1$'])
return (TN, FP, TN, FN), contingency_df
# 计算两个 percentCoherence 值下的列联表
(true_positive, false_positive, true_negative, false_negative), contingency_table = calculate_contingency_table(df_clean)
contingency_table
\(\hat{Y}=0\) |
\(\hat{Y}=1\) |
|
|---|---|---|
\(Y=0\) |
30 |
72 |
\(Y=1\) |
69 |
372 |
# 定义计算指标函数
def calculate_metrics(TP, FP, TN, FN):
# 计算准确性
accuracy = (TP + TN) / (TP + TN + FP + FN)
# 计算敏感性
sensitivity = TP / (TP + FN) if (TP + FN) != 0 else 0
# 计算特异性
specificity = TN / (TN + FP) if (TN + FP) != 0 else 0
return accuracy, sensitivity, specificity
# 计算指标
accuracy, sensitivity, specificity = calculate_metrics(true_positive, false_positive, true_negative, false_negative)
# 打印结果
print(f"True Positive: {true_positive}")
print(f"False Positive: {false_positive}")
print(f"True Negative: {true_negative}")
print(f"False Negative: {false_negative}")
print(f"准确性: {accuracy}")
print(f"敏感性: {sensitivity}")
print(f"特异性: {specificity}")
输出结果: True Positive: 30 False Positive: 72 True Negative: 30 False Negative: 69 准确性: 0.29850746268656714 敏感性: 0.30303030303030304 特异性: 0.29411764705882354
可以看出,这里的准确率和敏感性都不是很高。由于在这个示例中我们是使用每一种条件下后验分布的均值进行计算,并未考虑整个后验分布。大家可以思考一下,如果考虑所有整个后验分布后,预测的结果是否会发生变化?
如果新数据的自变量是一个新的取值呢?
当前我们只考虑了percentCoherence为10或40。我们还可以进一步探究当percentCoherence为25时的判断正确率,即\(X_i=25\)。
🔔注意:
需要注意的是,我们的自变量percentCoherence是连续变量,但是我们在编码的时候仍然按照离散变量的标准进行设定,即按照treatment coding 的方式进行0和1的编码。
因此,这里可能存在一些问题,我们在处理连续变量的时候实际上不需要做这种编码,而是直接带入自变量取值即可。
例如,当新数据的自变量取值为\(X_i=25\)时,我们直接将其带入进方程即可,而不需要将其按照离散变量编码为0.5。需要注意的是,新带入的数据需要和最开始建模数据的单位保持一致。
补充:使用bambi建立logistic回归模型#
这里我们使用bambi 提供的默认先验来构建模型。 可以看到:
先验为:
Intercept ~ Normal(mu: 0.0, sigma: 3.6269)
C(percentCoherence) ~ Normal(mu: 0.0, sigma: 5.0062)
模型分布为:bernoulli
链接函数为:p = logit
C(percentCoherence) 代表将 percentCoherence 变量编码为分类变量 (categorical variable)。
def inv_logit(log_odds):
return np.exp(log_odds) / (1 + np.exp(log_odds))
import bambi as bmb
bambi_logit = bmb.Model("correct ~ C(percentCoherence)", df_clean, family="bernoulli")
bambi_logit
模型拟合
这里使用 bambi 提供的默认拟合设置。
包括 4 条 MCMC 链,每个链 2000 个迭代,其中前 1000 个为 burn-in 阶段。
model_fitted = bambi_logit.fit(random_seed=84735)
model_fitted
fitted_parameters = az.summary(model_fitted)
fitted_parameters

由此可见,使用 bambi 建立的 logistic 回归模型得到的结果与我们使用 PyMC 建立的模型结果几乎一致:
C(percentCoherence)[40] 的均值为 1.762,与 beta_1 的均值 1.766 非常接近。
Intercept 的均值为 0.785,与 beta_0 的均值 0.784 差异微小。
p_coh10 = inv_logit( fitted_parameters.loc["Intercept", "mean"])
p_coh40 = inv_logit(
fitted_parameters.loc["Intercept", "mean"] + \
fitted_parameters.loc["C(percentCoherence)[40]", "mean"]
)
print(f"p(coherence=10) = {p_coh10:.3f}", f"p(coherence=40) = {p_coh40:.3f}")
posterior_predictive = bambi_logit.predict(model_fitted, kind="pps")
model_fitted
az.plot_ppc(model_fitted, num_pp_samples=50)
sns.despine()
总结
本节课学习了如何通过广义线性模型(Generalized linear model, GLM)拟合二元决策变量。
重点在于:
了解二元决策变量适合的分布,伯努利(Bernoulli)分布。
了解如何通过概率、发生率和链接函数(link function)来表示线性模型。
学习模型评估指标:准确性(Accuracy)、敏感性(Sensitivity)和特异性(Specificity)。