Part 2: Binomial与似然

二项数据模型 & 似然函数

确定先验之后，第二步，我们需要根据收集的数据构建似然函数

• 我们选取了 Evans 等(2020)的研究数据作为我们的案例展示，为计算方便，我们仅选取一名被试的数据，并对该被试数据进行选择以方便展示。

• 假设该被试的数据包含 50 次试验的随机点运动任务，我们希望通过 50 次的实验来估计被试在5%一致性条件下的判断正确的能力。

• 我们假设参与者的每一次判断是否正确是相互独立的。

• 假设参与者的正确判断次数为 Y，我们可以做出以下假设： 1、每次试验的正确与否是相互独立的（试验A的结果不会影响试验B，但实际实验当中会出现系列依赖效应，即前一个试次的正确性会影响后一个试次的判断，因此这个假定实际上是比较违背现实的）。 2、每次试验参与者正确判断的概率为ACC。

在这两个假设下，正确判断次数Y和正确率ACC之间的关系符合二项分布：

\( Y|ACC \sim Bin(50,ACC) \)

在不同正确率下，出现特定正确判断次数Y的概率 \( f(y|ACC)~~y \in \) { 0,1,2,…,50 }可以表示为：

\( f(y|ACC)=P(Y=y|ACC)=(^{50}_y) ACC^y(1-ACC)^{50-y} \)

我们来进行一些具体的计算：

• 假设ACC=0.1，那么在50次试验中，每个可能的正确判断次数\( Y\in (1,2,...,50) \)，而出现特定结果的概率可以表示为：

\( f(Y=1|π=0.1)=(^{50}_1)0.1^1(1-0.1)^{49} \) \( f(Y=2|π=0.1)=(^{50}_2)0.1^2(1-0.1)^{48} \)

…

\( f(Y=49|π=0.1)=(^{50}_{49})0.1^{49}(1-0.1)^1 \) \( f(Y=50|π=0.1)=(^{50}_{50})0.1^{50}(1-0.1)^0 \)

我们可以把这50个概率值画出来:

# 创建一个 Binomial 分布，参数为 n=50（试验次数），p=0.1（正确率概率）
binom = pz.Binomial(n=50, p=0.1)

# 绘制该分布的概率密度函数 (PDF)
binom.plot_pdf()

# 移除图的上边框和右边框
sns.despine()

# 显示图表
plt.show()

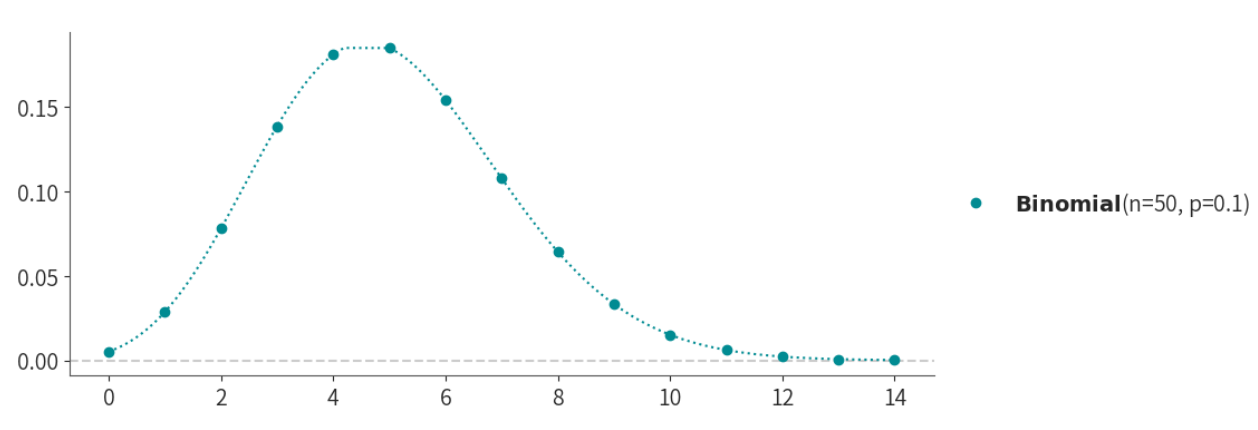
随机点运动任务中的正确率分布

• 在随机点运动任务中，正确率描述了参与者正确判断点运动方向的概率。在不同的正确率下，参与者在50次实验中正确判断的次数Y会有不同的分布情况。

我们可以模拟不同的ACC，并展示每个ACC下，正确判断次数Y的分布图。

（注：这里只展示了当正确率ACC=0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9 九种情况下的分布图，但是记住ACC的取值其实是[0,1]之间的任意数，有无穷多个的）

# 导入必要的库
import numpy as np
import pandas as pd
from scipy.stats import binom
import seaborn as sns
import matplotlib.pyplot as plt

# 设置二项分布的参数
n = 50  # 总试验次数
p_values = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]  # 不同的 p 值列表
k = np.arange(0, 51)                                      # 创建一个包含从0到50的整数的数组

# 创建一个包含 'Y' 列的 DataFrame
dist_all_pi = pd.DataFrame({'Y': k})

# 计算每个 'Y' 对应的概率，并将结果存储在相应列中
for p in p_values:
    column_name = f'{p}'
    dist_all_pi[column_name] = dist_all_pi['Y'].apply(lambda x: binom.pmf(x, n, p))

# 使用 stack() 和 reset_index() 转换数据为长格式
melted_data = dist_all_pi.set_index('Y').stack().reset_index()
melted_data.columns = ['Y', 'p', 'prob']

# 创建一个 FacetGrid 对象，用于绘制子图
plot_all_pi = sns.FacetGrid(melted_data, col='p', col_wrap=3)

# 使用柱状图绘制概率分布
plot_all_pi.map(sns.barplot, 'Y', 'prob', color="grey", order=None)

# 设置 x 和 y 轴的刻度和范围
plot_all_pi.set(xticks=[0, 10, 20, 30, 40, 50],
                yticks=[0.00, 0.05, 0.10, 0.15],
                ylim=(0, 0.20))

# 设置 y 轴标签
plot_all_pi.set_ylabels("$f(y|ACC)$")

# 设置子图的标题模板
plot_all_pi.set_titles(col_template="Bin(50,{col_name})")

# 显示x=30的点
# for ax in g.axes.flat:
#     ax.scatter(x=30, y=0, color='red', marker='o', s=60)
# g.show()

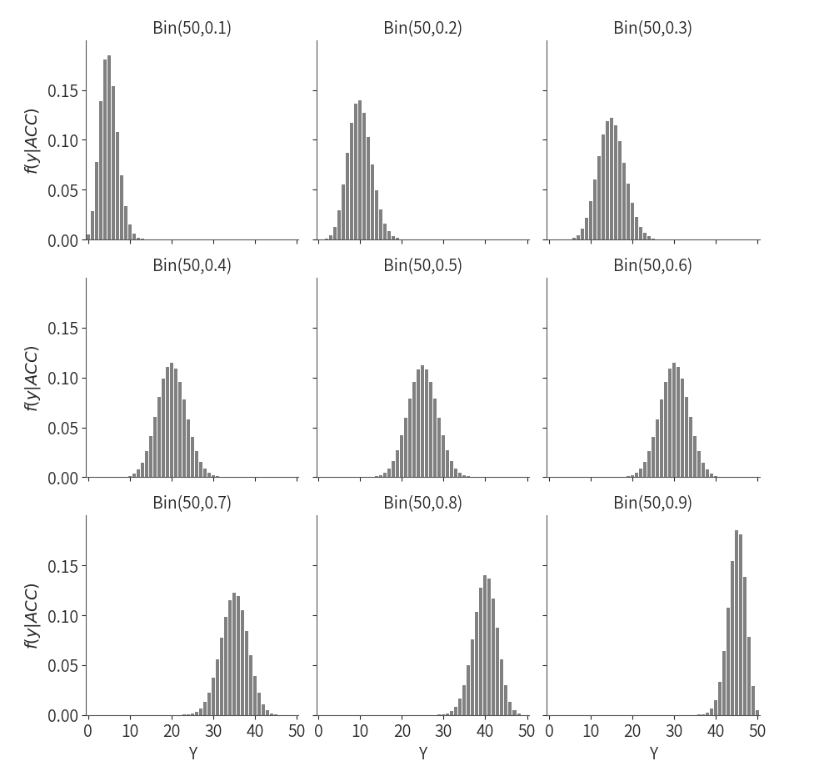
  上图可以看出，随着ACC的增大，ACC越高，正确判断次数高的情况越可能出现；相反，ACC越低，正确判断次数低的情况则更可能出现，这很符合我们的直觉。

  在随机点运动任务中，假设参与者在50次试验中有30次正确（即Y=30），我们可以写出在不同正确率ACC下发生这一结果的可能性，具体公式如下：

\(f(Y=30|ACC=0.1)=(^{50}_{30})0.1^{30}(1-0.1)^{20}\)

\(f(Y=30|ACC=0.2)=(^{50}_{30})0.2^{30}(1-0.2)^{20}\)

……

\(f(Y=30|ACC=0.8)=(^{50}_{30})0.8^{30}(1-0.8)^{20}\)

\(f(Y=30|ACC=0.9)=(^{50}_{30})0.9^{30}(1-0.9)^{20}\)

我们可以仅仅关注各个正确率下，正确判断次数Y=30发生的概率（下图黑点）

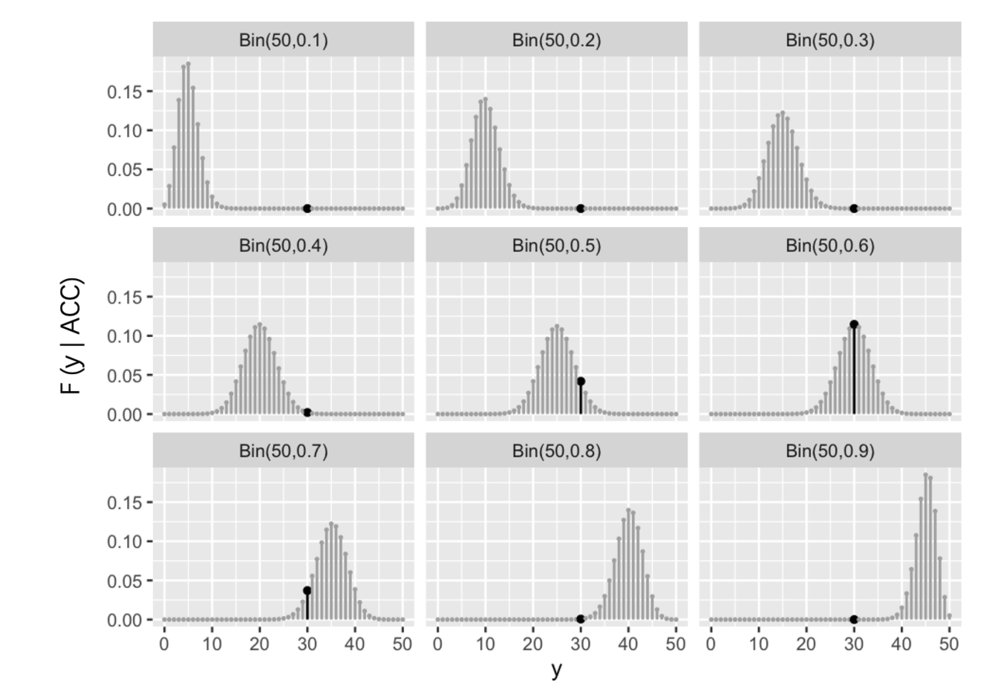
• 思考：上面的分布图中Y=30对应的可能性应当叫做概率还是似然？

  大家可以发现，我们现在已经得到了一个真实的数据，即Y=30。那么对于这个Y值而言，我们计算了不同ACC条件下Y=30发生的可能性，因此我们应当称其为似然。

似然函数

  将这些不同正确率下Y=30发生的相对可能性组合在一起，就构成了一个关于正确率的似然函数（\(L(ACC|Y=30)\)）：

\(L(ACC|Y=30)=(^{50}_{30})ACC^{30}(1-ACC)^{20}~for~ACC\in[0,1]\)

• 随机点运动任务中的正确率：

  通过绘制Y=30时，不同ACC下的相对可能性（即似然函数），我们可以观察到某个特定的ACC值最大化了这个似然函数。例如，可能在ACC=0.6时，似然函数达到了最大值，说明Y=30这一结果最有可能出现在ACC=0.6的情况下。

  因此，我们可以对[0,1]之间所有ACC进行取值，并将每个ACC条件下对应的Y=30出现的概率可视化出来，最后将其绘制成一条曲线：

import seaborn as sns
from scipy.special import comb

# 定义似然函数
def likelihood(ACC, Y=30, N=50):
    return comb(N, Y) * (ACC**Y) * ((1-ACC)**(N-Y))

# 定义ACC范围在[0, 1]之间
ACC_values = np.linspace(0, 1, 1000)

# 计算每个ACC对应的似然值
likelihood_values = likelihood(ACC_values)

# 设置Seaborn的绘图样式
sns.despine() # 移除图的上边框和右边框

# 绘制似然函数，使用Seaborn的绘图功能
sns.lineplot(x=ACC_values, y=likelihood_values, color="grey", label="Likelihood L(ACC | Y=30)")

# 设置图表标题和标签
plt.xlabel("ACC")
plt.ylabel("Likelihood")

# 在ACC=0.6处画出一条虚线
plt.axvline(x=0.6, color='red', linestyle='--', label="ACC=0.6 (Max)")

# 显示图例
plt.legend()
# 展示图表
plt.show()

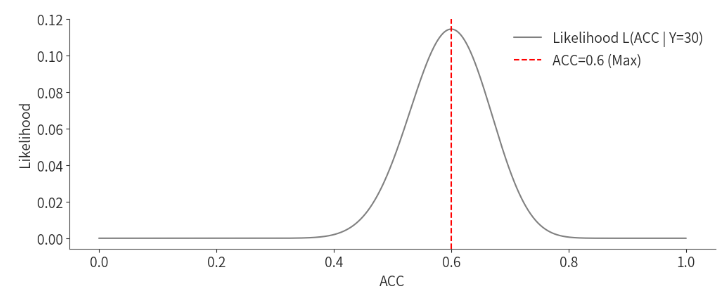
• 可以清晰地看出，当ACC=0.6时Y=30出现的可能性最大，并且Likelihood相加不太可能等于1，很容易就超过1了。