部分池化(Partial pooling)

部分池化(Partial pooling)#

  • 完全池化模型仅考虑了trial之间的差异，没有考虑被试之间的差异。

  • 非池化模型考虑了被试的差异，但是容易受到不同被试内部极端数据的影响，忽视了不同被试做同一任务时可能存在的关系。

部分池化 (Partial pooling)是构建分层模型的关键

  • 它假设，不同被试 (layer2) 来自于一个关于被试的总体 (Population)，被试形式的分布提供了对于组间变异(between variability)的解释。

  • 不同trial的反应时 (layer1) 又来自于不同被试 (layer2) ，每个被试内部的trial数形成的分布提供了对于组内变异(within variability)的解释。

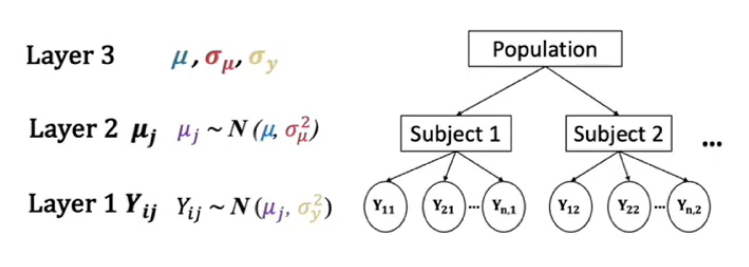
alt text

  • \(Layer1 —— 数据层\)

首先，第一层是反应时数据，\(Y_{ij}\)中的j是指第j个被试，i是指第j个被试的第i个数据点。我们假定每个被试的i个数据点都服从该被试自己的一个特定的正态分布，并且假定被试之间只是在均值上有差异，而方差相同，即每个被试的\(\sigma_y^2\)相同

  • \(Layer2 —— 被试层\)

数据层中每个被试的\(\mu_j\)也要服从一个更大的群体层面的正态分布 \(N(\mu,\sigma_\mu^2)\)。然而，这个正态分布并非直接对应数据，而是对应参数，即参数分布的参数，在层级模型里我们称之为“超参”，这里的超参则是\(\mu,\sigma_\mu^2\)。

  • \(Layer3 —— 群体层\)

\(\mu,\sigma_\mu,\sigma_y\)（总共有3个未知的参数）

\(\mu\)表示总体的反应时均值

\(\sigma_\mu\)表示组与组之间在Y均值上的变异性

\(\sigma_y\)表示每个组内部Y的变异性（我们假设每个组内部的变异性相同）

另一种定义方式

我们也可以这样来理解层级模型：

  • \(\mu_i\)表示：第j个被试的反应时均值

  • \(\sigma_\mu\)表示：第j个被试的反应时标准差

  • 那么，\(\mu_j与\mu\)的关系式可以写为：

\[ \mu_j=\mu+b_j \]

个体均值相对于总体均值存在一个偏倚量或者偏差：\(b_j\)

  • 同时，\(b_j\)满足：

\[ b_j \sim N(0,\sigma_\mu^2) \]

  • 那么层级模型的Layer1和Layer2可以写为：

\[\begin{split} Y_{ij}|\mu_j,\sigma_y \sim N(\mu_j,\sigma_y^2) ~~with~~\mu_j=\mu+b_j\\ b_j|\sigma_\mu \overset{ind}{\sim} N(0,\sigma_\mu^2) \end{split}\]

由于正态分布具有可加性，因此这两种定义方法都是可以的。

模型定义及MCMC采样

根据公式定义模型：

Layer1：\(Y_{ij}|\mu_j,\sigma_y \sim N(\mu_j,\sigma_y^2)\)观测数据由群组参数生成

Layer2：\(\mu_j|\mu,\sigma_\mu \overset{ind}{\sim} N(\mu,\sigma_\mu^2)\)生成不同被试的均值

Layer3：\(\mu,\sigma_y,\sigma_\mu\) 超参数

\[\begin{split} \mu \sim N(7.5,5^2)\\ \sigma_y \sim Exp(1)反应时在组内的变异性\\ \sigma_\mu \sim Exp(1)均值在组间的变异性 \end{split}\]

  • 相对于非池化模型，部分池化模型的关键在于定义，被试参数在总体上的变异，即mu = pm.Normal("mu", mu=hyper_mu, sigma=var_mu, dims="subject")。

  • 其次，是相似于非池化模型，trial数的反应时间分布在被试上的变异 pm.Normal("y_est", mu=mu[subject_id], sigma=var_y, observed=log_RTs, dims="obs_id")。

# 建立被试 ID 映射表
subject_mapping = {subj_id: idx for idx, subj_id in enumerate(df_first5["subj_id"].unique())}

# 将被试 ID 转换为索引
mapped_subject_id = df_first5["subj_id"].map(subject_mapping).values

# 定义 pymc 模型坐标
coords = {
    "subject": df_first5["subj_id"].unique(),
    "obs_id": df_first5.index.values
}

with pm.Model(coords=coords) as partial_pooled_model:
    
    # 对 RT 进行 log 变换
    log_RTs = pm.MutableData("log_RTs", np.log(df_first5['RT']))

    # Hyperpriors,定义全局参数——我们主要想估计的参数
    var_y = pm.Exponential("within_variability", 1)
    var_mu = pm.Exponential("between_variability", 1)
    hyper_mu = pm.Normal("hyper_mu", mu=7.5, sigma=5)

    # 定义被试参数
    mu = pm.Normal("mu", mu=hyper_mu, sigma=var_mu, dims="subject")
    #获得观测值对应的被试映射
    subject_id = pm.MutableData("subject_id", mapped_subject_id, dims="obs_id")
    # 定义 likelihood
    likelihood = pm.Normal("y_est", mu=mu[subject_id], sigma=var_y, observed=log_RTs, dims="obs_id")

    partial_trace = pm.sample(draws=5000,                   # 使用mcmc方法进行采样，draws为采样次数
                                tune=1000,                    # tune为调整采样策略的次数，可以决定这些结果是否要被保留
                                chains=4,                     # 链数
                                discard_tuned_samples= True,  # tune的结果将在采样结束后被丢弃
                                random_seed=84735)

pm.model_to_graphviz(partial_pooled_model)

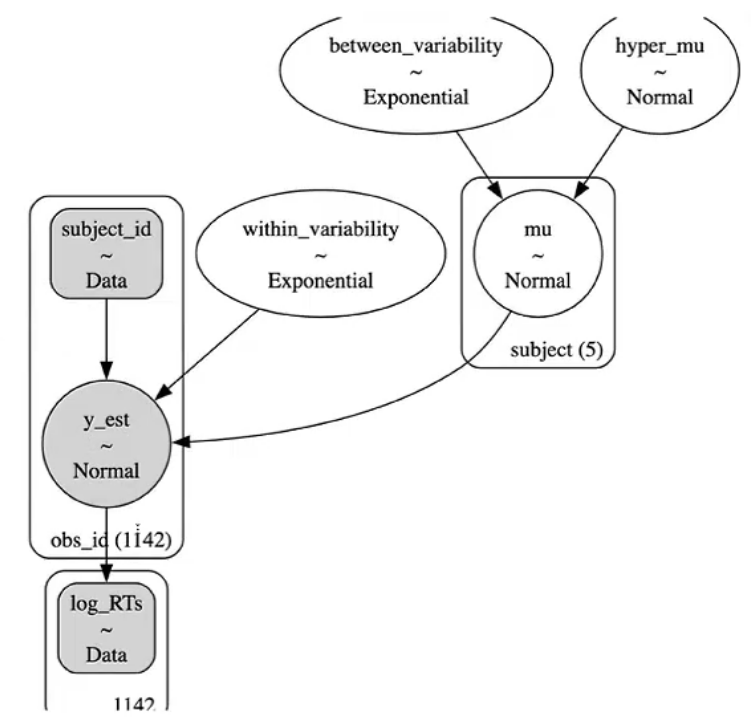
alt text

模型的结构：

  • 每个被试的反应时均值是由两个超参得到的：分别是群体层面的\(\mu\)和被试间的变异性\(\sigma_\mu\)。

  • 另一个参数则是被试内的变异性\(\sigma_y\)

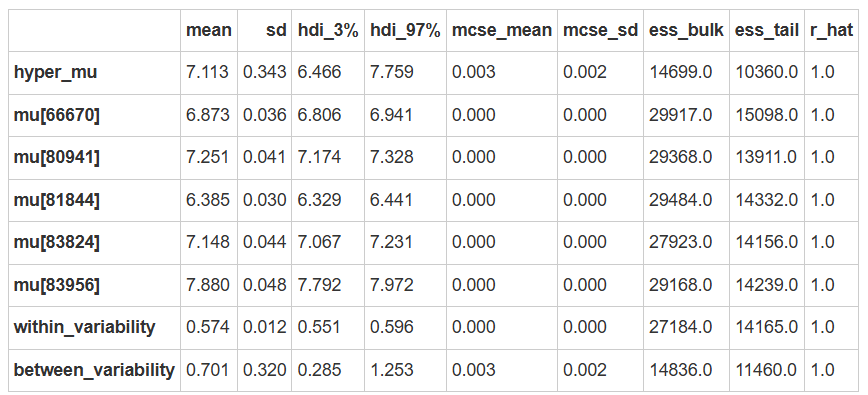
查看后验参数估计

可以发现:

  • 不同被试的反应时间具有一致性，组内变异较小（较小的标准差）。

  • 被试均值存在显著差异，表明被试间的反应时间差异显著。

az.summary(partial_trace)

alt text

ax = az.plot_trace(
    partial_trace,
    var_names=["mu"],
    filter_vars="like",
    compact=False,
    figsize=(7,14))
plt.tight_layout()

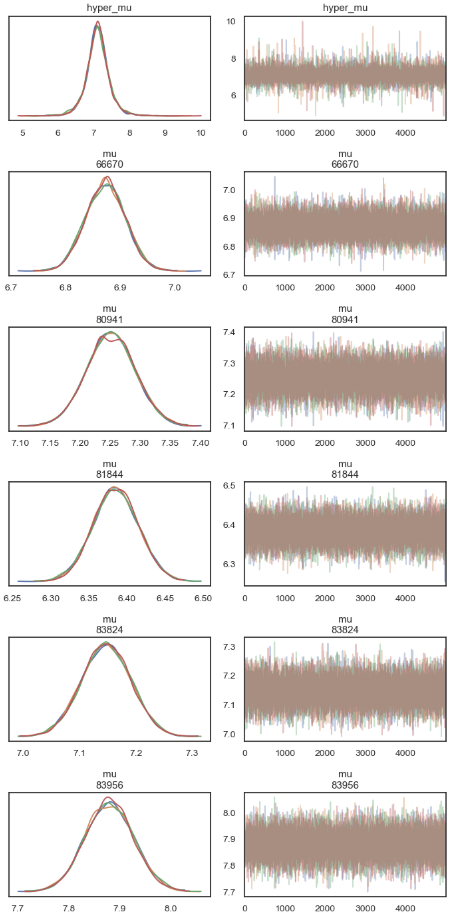
alt text

后验预测分布

partial_ppc = pm.sample_posterior_predictive(partial_trace,
                                            model=partial_pooled_model)

partial_hdi_sum = ppc_sum(ppc=partial_ppc,
                  data=df_first5)

同样进行对数转换：

partial_hdi_sum = inv_log_hdi_sum(partial_hdi_sum)

可视化预测结果：

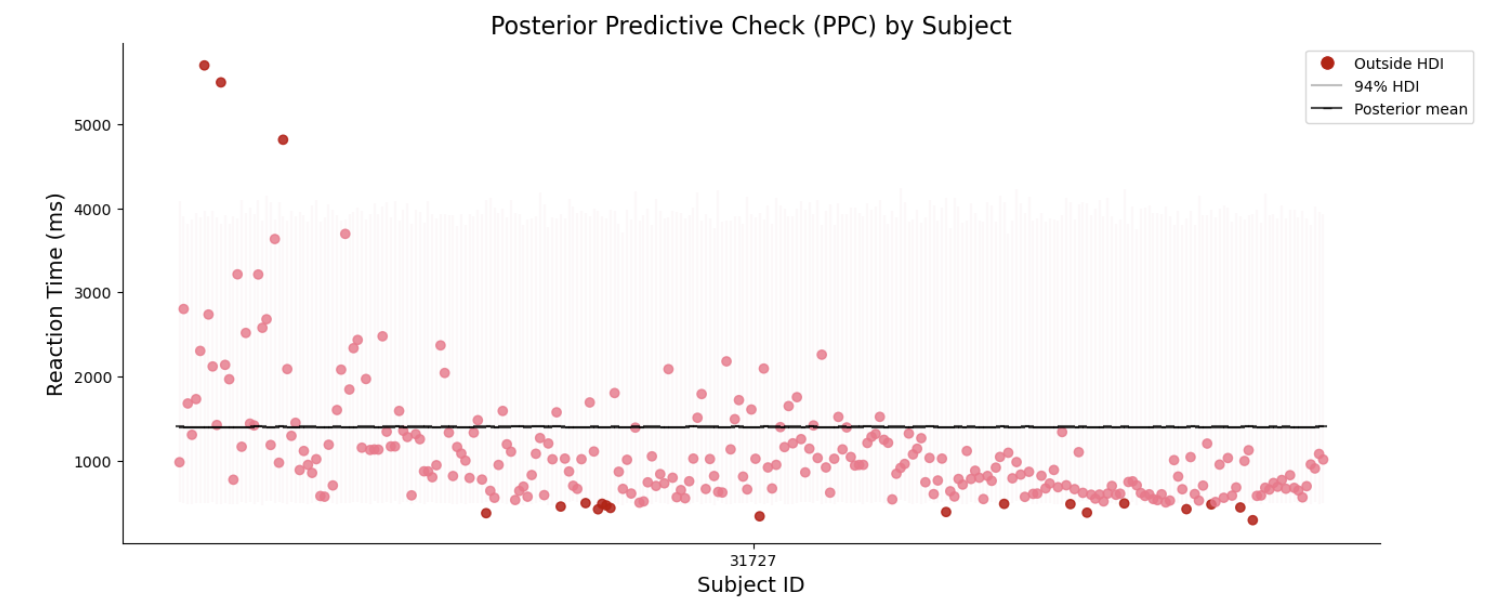
ppc_plot(hdi_sum=partial_hdi_sum)

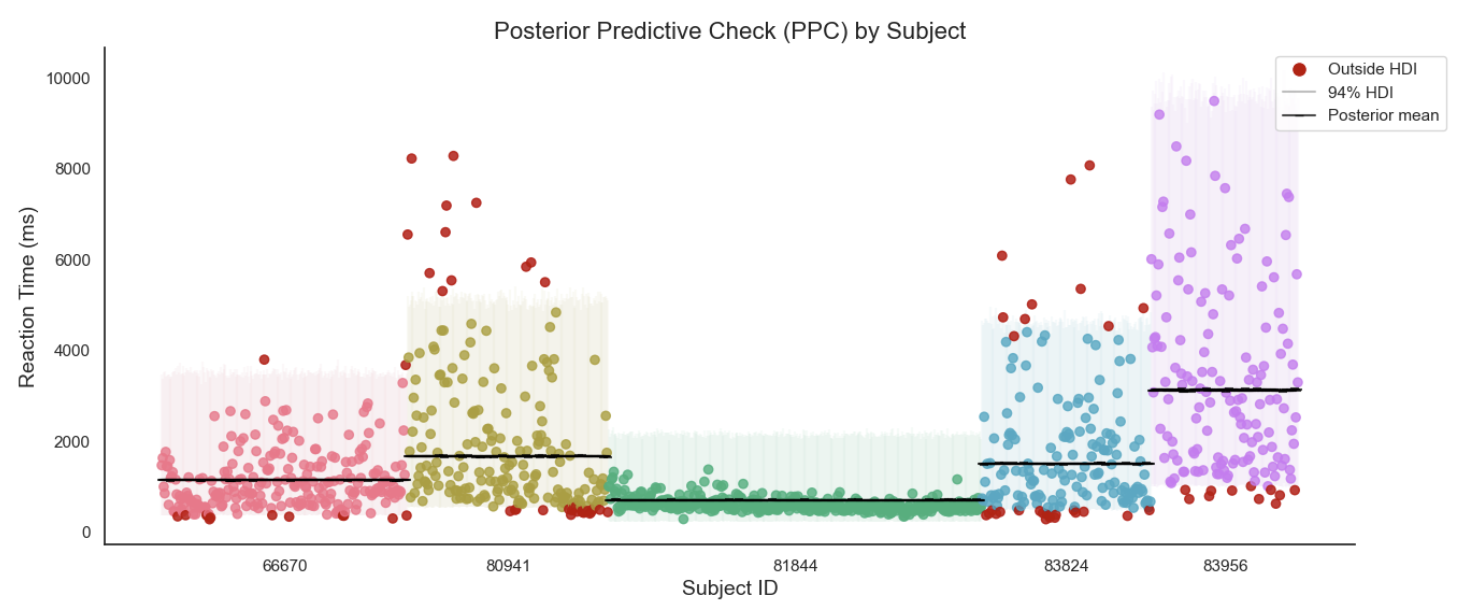
alt text

  • 可以看到相比于非池化模型，在层级模型中不同组的后验预测可信区间的长度、后验预测均值都更为接近。

我们将三种模型放在一起对比：

fig, axes = plt.subplots(3,1, figsize=(7,9))

ax = axes[0]
ax = ppc_plot(hdi_sum=complete_hdi_sum, ax = ax, show_plot=False)
ax.set_title("Complete pooling model")

ax = axes[1]
ax = ppc_plot(hdi_sum=partial_hdi_sum, ax = ax, show_plot=False)
ax.set_title("Patial pooling model")

ax = axes[2]
ax = ppc_plot(hdi_sum=no_hdi_sum, ax = ax, show_plot=False)
ax.set_title("No pooling model")

sns.despine()
plt.tight_layout()
plt.show()

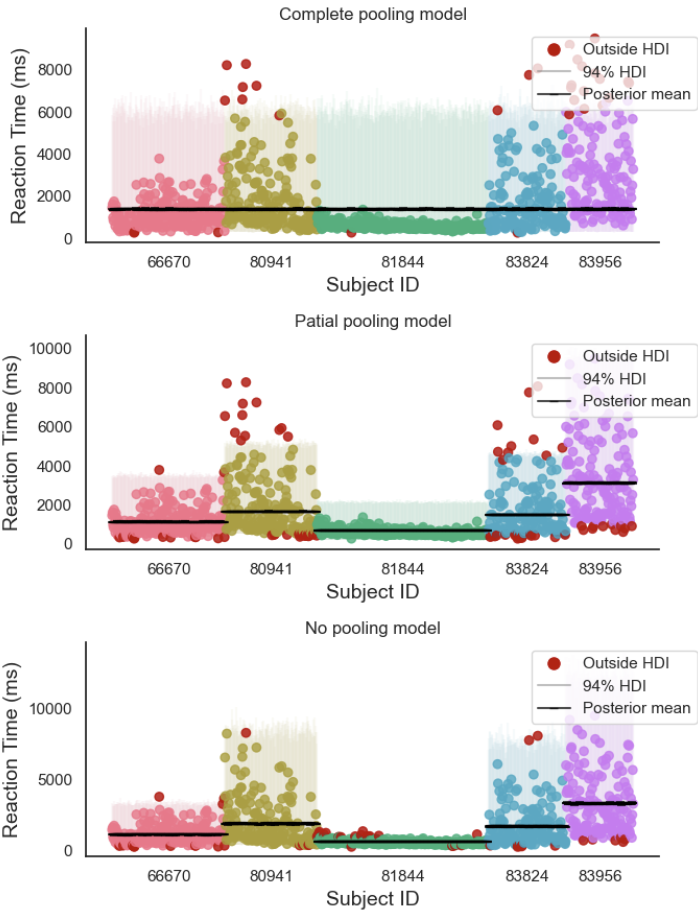
alt text

  • 可以明显看出，相比于完全池化模型和非池化模型，部分池化模型事先了一个较好的折中。

Within- vs between-group variability#

  • 在完全池化模型中，变异性的来源只有一种，即个体观测值\(Y\)在总体中的变异 (\(σ\))

  • 在非池化模型中，变异来源分散在不同被试中，即个体观测值在不同被试中的变异 (\(\sigma_j\))

而在部分池化模型中，我们可以把个体观测值\(Y\)的变异来源分解成两个部分：

  • 组内（被试内）变异：\(\sigma_y\)

是指在每个被试内部，不同试次之间的变异性。

  • 组间（被试间）变异：\(\sigma_\mu\)

是指被试与被试之间在均值上的变异性，可以理解为个体差异。

\[ Var(Y_{ij})=\sigma_y^2+\sigma_\mu^2 \]

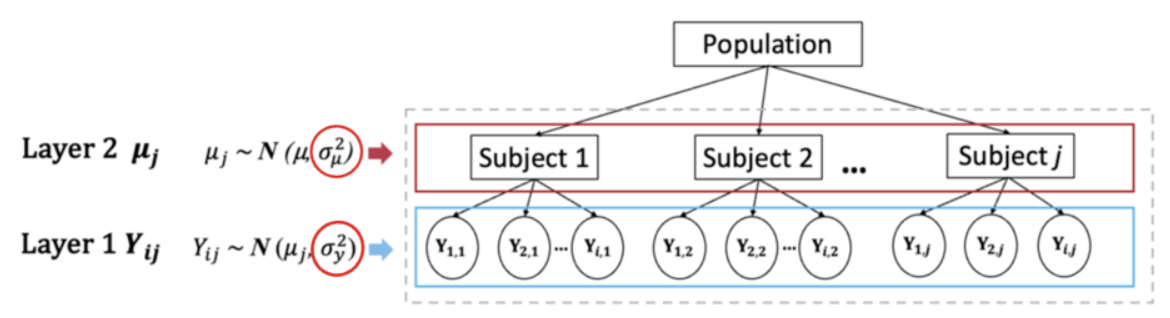
alt text

我们可以通过类似于单因素方差分析的方法，计算出总变异性被被试间或被试内变异所解释的比例。

\[ \frac{\sigma_y^2}{\sigma_\mu^2+\sigma_y^2}=总变异可以被组内方差解释的部分 \]
\[ \frac{\sigma_\mu^2}{\sigma_\mu^2+\sigma_y^2}=总变异可以被组间方差解释的部分 \]

  • 如果组间方差远大于组内方差，那么组间方差可以解释大部分观测值的变异，即个体差异较大。

  • 如果组间方差远小于组内方差，那么组间的区别就不是很明显，即被试之间接近于同质的。

此外，若组间方差远大于组内方差，则可以说明组内的变异性很小，组内分数高度相关：

\[ Cor(Y_{ij},Y_{kj})=\frac{\sigma_\mu^2}{\sigma_\mu^2+\sigma_y^2} \]

  • 这意味着我们可以计算跨时间节点、跨条件的个体差异是否稳定，也可以把它变成一个和信度指标相关的计算公式。如果感兴趣，可以查阅一个叫做icc(interclass correlation)的指标。

下图展示了三种组间方差与组内方差的分布情况(横轴为方差的大小，蓝色为组间方差，黑色为组内方差)：

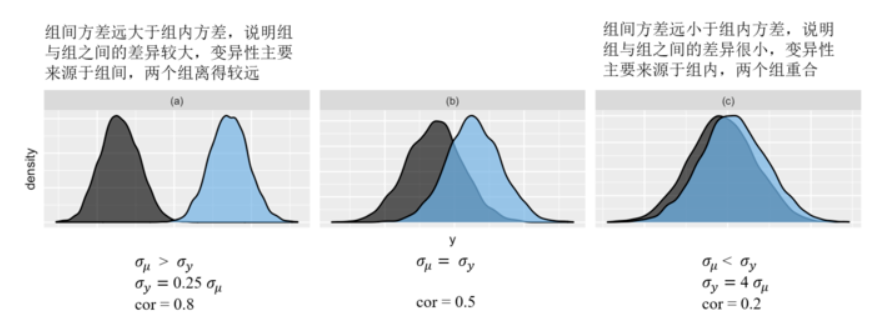
alt text

  • 组别越独特，\(\sigma_\mu\)相对越大，每组内的相关性就越大。

  • 图 (a) 中，组间变异是组内变异的4倍，此时组内相关性为 0.8，接近于 1。

  • 图 (c) 中，组间变异是组内变异的1/4倍，组内相关性为 0.2，接近 0。

Shrinkage & the bias-variance trade-off#

从下图和表格中可以发现:

  • 对于目前的被试来说，相比于非池化模型，部分池化模型中的参数更加靠近完全池化模型，这就是分层模型的收缩 (shrinkage) 现象。

# 提取三个模型参数后验，筛选中其中含有mu参数的部分
partial_stats = az.summary(partial_trace, var_names=["mu"], filter_vars = "like", kind="stats")
no_stats = az.summary(no_pooled_trace, var_names=["mu"], filter_vars = "like", kind="stats")
complete_stats = az.summary(complete_trace, var_names=["mu"], filter_vars = "like", kind="stats")

partial_stats = inv_log_hdi_sum(partial_stats)
no_stats = inv_log_hdi_sum(no_stats)
complete_stats = inv_log_hdi_sum(complete_stats)

# 设置一列，表明参数来源
complete_stats['source'] = 'Complete pool'
no_stats['source'] = 'No pool'
partial_stats['source'] = 'Partial pool'

# 合并三个模型的结果
df_compare = pd.concat([complete_stats.reset_index(),
                        no_stats.reset_index(),
                        partial_stats.reset_index()])

#设置索引，表明参数来源
df_compare.set_index(['source', df_compare.index], inplace=True)
df_compare

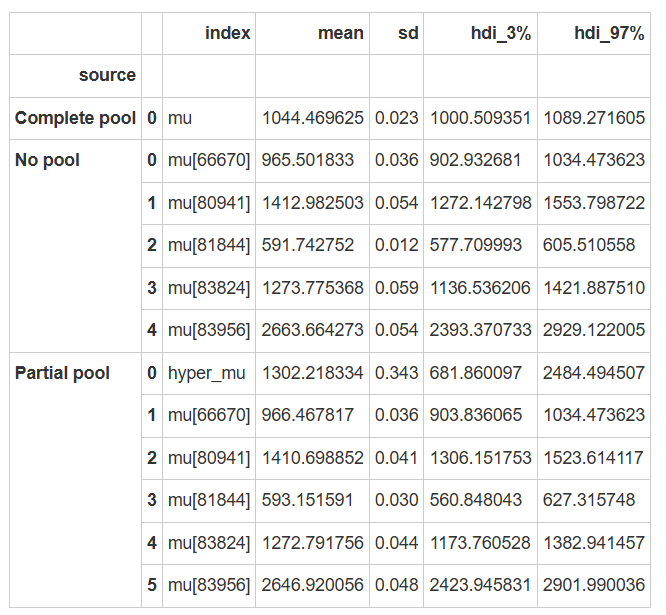
alt text

# 设置三个绘制坐标轴
fig, (ax1, ax2, ax3) = plt.subplots(1,3, figsize=(12,4), sharex=True)

# 绘制三个模型参数后验
az.plot_forest(partial_trace, var_names=["mu"], filter_vars = "like", combined=True, ax=ax1)
ax1.set_title("Patial Pooling")
az.plot_forest(no_pooled_trace, var_names=["mu"], filter_vars = "like", combined=True, ax=ax2)
ax2.set_title("No Pooling")
az.plot_forest(complete_trace, var_names=["mu"], filter_vars = "like", combined=True, ax=ax3)
ax3.set_title("Complete Pooling")

plt.tight_layout()
plt.show()

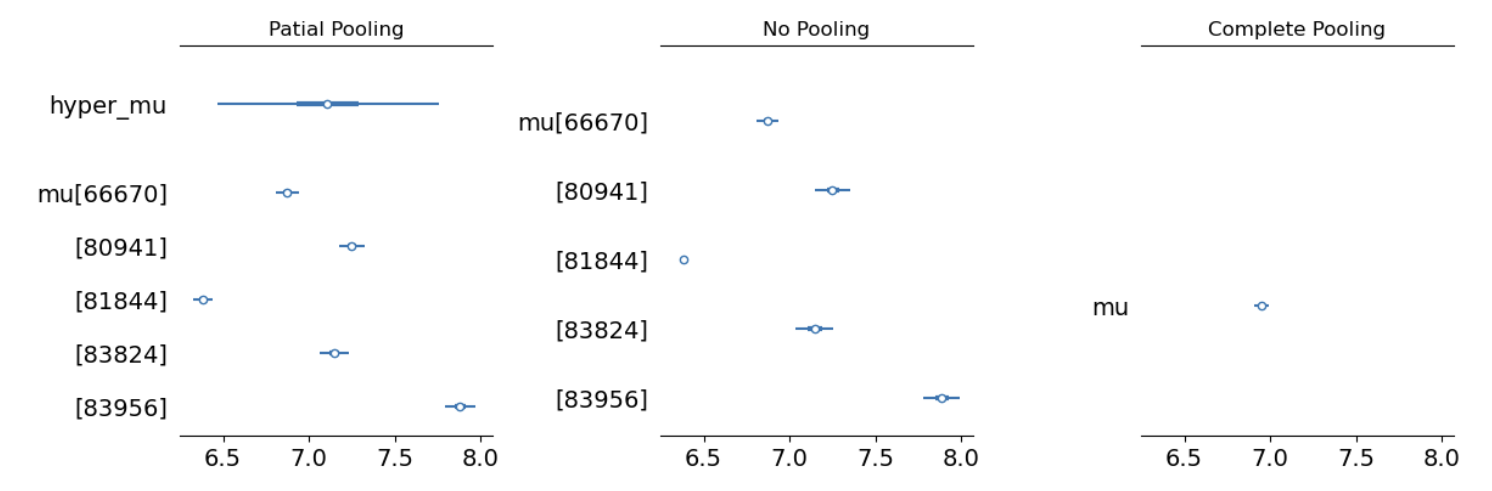
alt text

  • 在完全池化模型中，对于每一个被试来说，后验估计均值都是相同的，在弱先验的情况下，后验估计均值约等于所有观测值的平均值。

\[ \overline{y}_{global}=\frac{1}{n}\sum_{all~i,j}y_{ij} \]

  • 在非池化模型中，对于每一个被试来说，其后验估计均值的估计只来自该组内部，在弱先验的情况下，后验估计均值约等于该组内所有观测值的平均值。

\[ \overline{y}_j=\frac{1}{n_j}\sum^{n_j}_{i=1}y_{ij} \]

  • 在层级模型中，后验估计均值则是在完全池化和非池化模型中找到一个平衡，组间(group-specific)参数有可能更倾向完全池化模型，也有可能更倾向于非池化模型，这种现象被称为shrinkage

我们可以发现，在部分池化模型中，每个被试的数据向总体均值的方向拉取，会向内发生收缩，所以叫做“shrinkage”。

  • 当使用弱信息先验时，分层模型的后验平均预测结果（大致）是完全池化模型和非池化模型预测结果的加权平均

\[ \frac{\sigma_y^2}{\sigma_y^2+n_j\sigma_\mu^2}\overline{y}_{global}+\frac{n_j\sigma_\mu^2}{\sigma_y^2+n_j\sigma_\mu^2}\overline{y}_j \]

我们可以分别绘制出每个观测值对应的后验预测均值，并观察这些后验预测均值在不同的模型之间发生了什么变化:

#设置画布大小1
plt.figure(figsize=(9,4))

#绘制完全池化模型下每个点对应的后验预测均值
plt.scatter(complete_hdi_sum["obs_id"],
            complete_hdi_sum["mean"],
            alpha=0.15,
            s=80,
            label="Complete pooling")

#绘制非池化模型下每个点对应的后验预测均值
plt.scatter(no_hdi_sum["obs_id"],
            no_hdi_sum["mean"],
            alpha=0.15,
            s=80,
            label="No pooling")

#绘制部分池化模型下每个点对应的后验预测均值
plt.scatter(partial_hdi_sum["obs_id"],
            partial_hdi_sum["mean"],
            alpha=0.15,
            s=80,
            label="Partial pooling")

#设置图例
plt.legend()

#计算每个被试的数据量，并根据数据量大小在x轴上进行刻度标识
count_per_subject = df_first5.groupby("subject").size().values
cumulative_count = count_per_subject.cumsum()
xtick = cumulative_count - count_per_subject / 2
plt.xticks(xtick,df_first5["subject"].unique())

#设置标题
plt.title("Posterior mean of observed data",
          fontsize=15)
sns.despine()

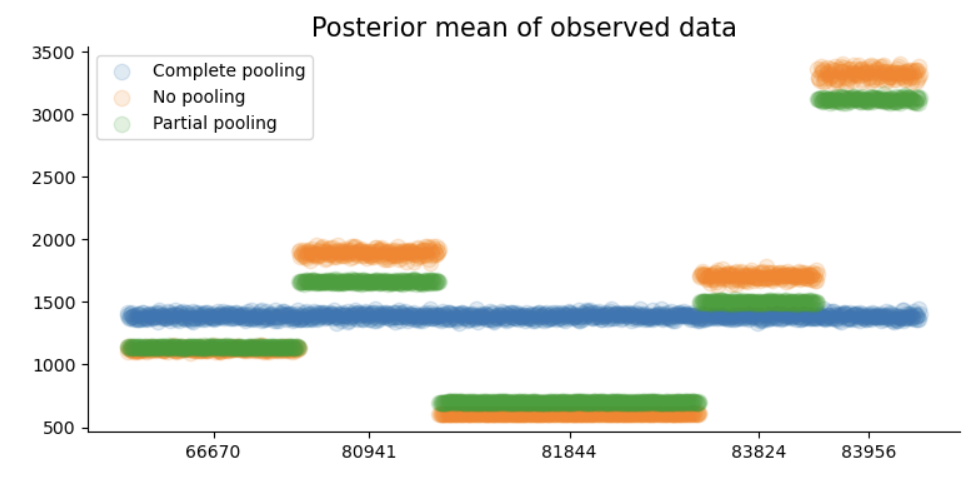
alt text

  • 收缩的大小 (即完全池化模型均值和非池化模型均值的权重)，取决于被试的数量\(n_j\)以及组内和组间变异性的比值。

    • 当被试的数量减少后，收缩率会增加。即我们越来越依赖全局的趋势来了解一个组别较少的结果。

    • 当组内变异性\(\sigma_y\)和组间变异性\(\sigma_\mu\)比值较大时，收缩率也会增加。即当被试之间的差异很小时，我们会更依赖于用全局的趋势来理解其中一个被试的数据。

层次模型在完全池化和无池化之间取得了平衡，优势在于：

1.将对不同群体(被试)的观察结果推广到更广泛的总体中

2.在了解任何单个群体时，借用所有其他群体的信息

这也导致了它的缺点：

  • 如果被试数量少，并且组内变异大，那么我们对于总体和不同组别(被试)的估计都可能存在偏差。

完全池化

非池化

部分池化

特点

仅考虑总体的变异，模型过于简单

仅考虑各组别的差异，结果难以推广到总体

同时考虑组间和组内变异

偏差-方差权衡

有较高的偏差和较低的方差

较低的偏差和较高的方差

更为平衡

模型评估

接下来，我们通过MAE指标对三个不同的模型进行评估，以比较它们的表现：

def calculate_mae(hdi_sum, obs = "y", pred = "mean"):
    """
    计算后验预测均值和 MAE (Median Absolute Error)。
    """

    # 提取后验预测值
    observed_data = hdi_sum[obs]
    posterior_predictive = hdi_sum[pred]
    
    # 计算 MAE（绝对误差的中位数）
    mae = np.median(np.abs(observed_data - posterior_predictive))
    
    return mae

pd.DataFrame({
    "Complate Pooling Model": [calculate_mae(complete_hdi_sum)],
    "No Pooling Model": [calculate_mae(no_hdi_sum)],
    "Partilar Pooling Model": [calculate_mae(partial_hdi_sum)],
})

Complate Pooling Model

No Pooling Model

Partilar Pooling Model

0

769.935022

402.799413

376.013831

预测新组的数据

  • 我们可以根据当前的层级模型对新组别的数据进行预测，如被试31727

  • 在pymc中，只要在pm.sample_posterior_predictive中传入层级模型的后验参数采样结果，即可以在层级模型的基础上对新数据生成预测

  • 预测结果储存在.predictions中

# 选择被试为"31727"的数据
new_data = df_raw[(df_raw.subject == 31727) & (df_raw['percentCoherence'] == 5)]

# 建立索引 'subj_id' 和 'obs_id'
new_data['subj_id'] = new_data['subject']
new_data['obs_id'] = new_data.groupby('subject').cumcount() + 1

new_data.head()

alt text

进行预测时，我们将使用新数据 new_data；以及先前模型计算出的参数，即：

\[\begin{split} hyper_mu=7.105\\ sd=0.349 \end{split}\]
# 建立被试 ID 映射表
subject_mapping = {subj_id: idx for idx, subj_id in enumerate(new_data["subj_id"].unique())}

# 将被试 ID 转换为索引
mapped_subject_id = new_data["subj_id"].map(subject_mapping).values

# 定义 pymc 模型坐标
new_coords = {
    "subject": new_data["subj_id"].unique(),
    "obs_id": new_data.index.values
}

with pm.Model(coords=new_coords) as partial_pooled_pred:
    
    # 对 RT 进行 log 变换
    log_RTs = pm.MutableData("log_RTs", np.log(new_data['RT']))

    # 定义新预测数据对应的新参数
    hyper_mu = pm.Normal("new_hyper_mu", mu=7.105, sigma=0.340)
    var_y = pm.Exponential("new_within_variability", 5)
    var_mu = pm.Exponential("new_between_variability", 5)

    # 定义被试参数
    new_mu = pm.Normal("new_mu", mu=hyper_mu, sigma=var_mu, dims="subject")
    #获得观测值对应的被试映射
    subject_id = pm.MutableData("subject_id", mapped_subject_id, dims="obs_id")
    
    # 定义 likelihood
    likelihood = pm.Normal("y_est", mu=new_mu[subject_id], sigma=var_y, observed=log_RTs, dims="obs_id")
    
    # 进行后验预测估计，注意使用的是上一个模型的后验参数估计，partial_trace
    pred_trace = pm.sample_posterior_predictive(partial_trace,
                                                var_names=["y_est"],
                                                predictions=True,
                                                random_seed=84735)

对预测数据进行转换并进行可视化：

pred_hdi_sum = ppc_sum(ppc=pred_trace.predictions,data=new_data)
pred_hdi_sum = inv_log_hdi_sum(pred_hdi_sum)
ppc_plot(pred_hdi_sum)

alt text

Contents