Bayes Factor

Bayes Factor#

  • 前面的课主要涉及贝叶斯统计的原理、基于后验的一系列分析和推断等内容，而这节课我们开始讲解前几课中经常提到的贝叶斯因子(Bayes Factor, BF)，实际上就是在贝叶斯学派的框架下进行的假设检验。

我们先简单回顾一下传统统计中的零假设显著性检验（Null Hypothesis Significance Test, NHST）

传统的假设检验方法#

频率学派的假设检验主要是基于概率性质的反证法所实现的推论统计方法。

———即承认如下前提:小概率事件(发生概率小于0.05的事件)在单次抽样中不会发生。

在传统的假设检验框架中，研究者需要根据研究对总体做互斥的两种假设，即零假设\(H_0\)和备择假设\(H_1\):

  • 零假设（Null Hypothesis，\(H_0\)）: 表示没有效应或差异的假设。在许多情况下，零假设代表“无差异”或“无效应”，例如认为两组数据的均值没有显著差异。

  • 备择假设（Alternative Hypothesis, \(H_1\)）：表示零假设不成立时的假设，通常认为有显著效应或差异。

传统假设检验的核心概念还包括：

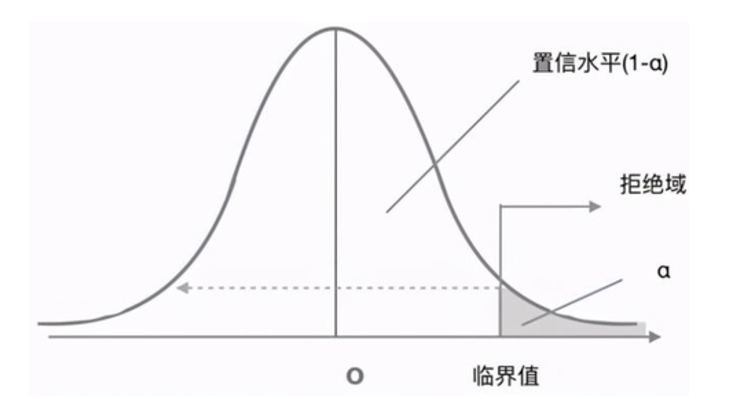
  • Alpha（\(\alpha\)）：显著性水平，通常设定为0.05，表示在零假设(\(H_0\))成立的情况下，错误拒绝\(H_0\)的概率。换句话说，alpha（\(\alpha\)）是我们愿意接受的一类错误概率（假阳性）。

  • \(P\)值：是指在零假设成立的前提下，观察到当前或更极端数据的概率。如果\(P\)值≤\(\alpha\)，传统统计学的框架下通常会拒绝零假设，认为数据提供了足够的证据支持备择假设。

传统的假设检验方法主要依赖于\(P\)值，这一方法在统计学中应用广泛，但也存在多个问题：

  • 假阳性结果：研究者可能会通过操纵p值来达到显著性，如增加样本量或调整变量，这会导致假阳性结果，误导后续研究。

  • 忽视效应大小：\(P\)值无法提供效应大小的信息，仅仅是显著与否的二分判断，不能全面反映数据的实际意义。

  • 不考虑先验信息：传统假设检验忽略了先验知识和理论背景，仅关注数据本身，无法有效利用已有的研究成果。

  • 无法为直接为零假设提供支持：不显著结果不代表零假设为真。

alt text

  • 胡传鹏等(2018). 贝叶斯因子及其在JASP中的实现. 心理科学进展

  • 吴凡, 顾全, 施壮华, 高在峰, 沈模卫. (2018). 跳出传统假设检验方法的陷阱——贝叶斯因子在心理学研究领域的应用. 应用心理学

🤔思考

  • 问题1：\(\alpha\)错误是漏报还是虚报？

答：这里我们将\(H_0\)看作是“没有信号”，\(H_1\)看作是“有信号”。那么，如果“无信号”成立，但我们却报告了“有信号”，这实际上是——虚报。

  • 问题2：假设\(P\)值为0.01，\(\alpha\)值为0.05，我们的一类错误的概率是多少？

答：依旧是0.05（\(\alpha\)）。

为什么要介绍贝叶斯因子？#

与传统假设检验方法相比，贝叶斯因子具有以下几方面的优势：

  • 1.对假设一视同仁： 同时评估\(H_0\)和\(H_1\)的可能性，能够为\(H_0\)提供支持证据，解决传统假设检验难以证明\(H_0\)成立的问题。

  • 2.结合先验信息： 贝叶斯因子分析可以利用先验知识，将前人的研究成果与当前数据结合，提供更为全面的证据评估。

  • 3.避免p值操纵： 贝叶斯因子的计算基于全数据集，不受单个数据点的影响，能够有效避免p值操纵带来的假阳性结果。而NHST则可以通过扩大样本量来使P值逐渐缩小至0.05，这可能会导致假阳性结果。

  • 4.支持多模型比较： 贝叶斯因子不仅适用于二元假设检验，还可以用于比较多个模型的适用性，提供更为灵活的统计分析工具。

  • 5.可以直接支持零假设。

吴凡, 顾全, 施壮华, 高在峰, 沈模卫. (2018). 跳出传统假设检验方法的陷阱——贝叶斯因子在心理学研究领域的应用. 应用心理学

贝叶斯因子（Bayes Factor，BF）的基本概念#

频率学派将随机事件发生的频率作为一种客观指标，而贝叶斯学派则从观察者的视角出发将概率理解为一种主观不确定性。

  • 贝叶斯因子（Bayes Factor，BF）作为一种基于贝叶斯统计的验证方法，主要用于比较零假设与备择假设的相对支持程度，其衡量的主要是数据在这两种假设下的解释能力。

具体来说，贝叶斯因子可以表示为：

\[ BF_{10}=\frac{posterior~odds}{prior~odds} = \frac{P(H_1|Data)}{P(H_0|Data)} * \frac{P(H_1)}{P(H_0)} = \frac{P(Data|H_1)}{P(Data|H_0)} \]

其中，\(P(Data|H_1)\)和\(P(Data|H_0)\)分别表示在备择假设和零假设下数据的似然性。

  • posterior odds：后验概率比

  • prior odds：先验概率比

  • \(H_0\)：零假设，\(H_1\)：备择假设

Heck, D. W., Boehm, U., Böing-Messing, F., Bürkner, P.-C., Derks, K., Dienes, Z., Fu, Q., Gu, X., Karimova, D., Kiers, H. A. L., Klugkist, I., Kuiper, R. M., Lee, M. D., Leenders, R., Leplaa, H. J., Linde, M., Ly, A., Meijerink-Bosman, M., Moerbeek, M., … Hoijtink, H. (2023). A review of applications of the bayes factor in psychological research. Psychological Methods, 28(3), 558–579. https://doi.org/10.1037/met0000454

当然，贝叶斯因子还有一种表达方式，即后验概率比等于贝叶斯因子乘以先验概率比：

\[ posterior~odds=BF_{10}×Prior~odds \]

  • 这说明，贝叶斯因子不仅反映了数据对假设的支持程度，还反映了先验概率到后验概率变化的程度或证据。简单来说，贝叶斯因子反映了当前数据更可能在\(H_0\)还是\(H_1\)下出现，这比较符合我们的直觉。

同时，贝叶斯因子分析能够帮助研究者根据现有证据评估不同假设成立的可能性之比，并且在评估证据强度上也有一套独立的标准：

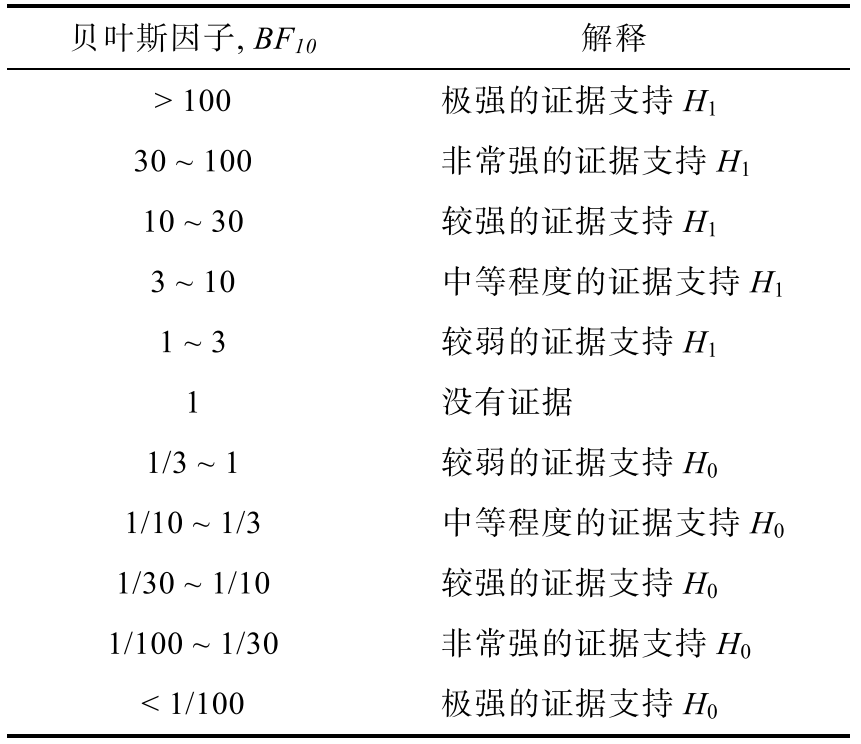
Source: 该表改编自胡传鹏等(2018)，源引用于Lee & Wagenmakers (2014)

  • \(BF_{10}=1\)，收集到的数据并没有改变备择假设\(H_1\)的相对可能性

  • \(BF_{10}>1\)，收集到的证据增加了备择假设\(H_1\)的相对可能性，BF越大，表明支持备择假设\(H_1\)的证据越强。

  • \(BF_{10}<1\)，收集到的证据削弱了备择假设\(H_1\)的相对可能性，BF越小，表明支持备择假设\(H_1\)的证据越弱。

需要注意：

  • 1.这只是一个大致的划分，而非绝对的标准。而在心理学研究当中，现在比较常用的两个标准是6和10。

  • 2.BF的下角标——“10”并不是指数字，而分别指代\(H_1\)和\(H_0\)

  • 胡传鹏, 孔祥祯, Eric-Jan Wagenmakers, Alexander Ly, 彭凯平. (2018). 贝叶斯因子及其在JASP中的实现. 心理科学进展

  • Makowski, D., Ben-Shachar, M. S., & Lüdecke, D. (2019). bayestestR: Describing Effects and their Uncertainty, Existence and Significance within the Bayesian Framework. Journal of Open Source Software, 4(40), 1541. https://doi.org/10.21105/joss.01541

  • Makowski, D., Ben-Shachar, M. S., Chen, S. H. A., & Lüdecke, D. (2019). Indices of Effect Existence and Significance in the Bayesian Framework. Retrieved from 10.3389/fpsyg.2019.02767

Contents