Lecture 5: Bayesian Inference: From Traditional Foundations to Current Practices

Lecture 5: Bayesian Inference: From Traditional Foundations to Current Practices#

👨‍💻内容回顾

单一事件、离散变量和连续变量中的贝叶斯公式#

知识点

内容描述

先验

似然

贝叶斯更新

感兴趣的目标

单个事件

一个使用特定语言风格的心理学实验被成功重复出来的可能性

OSC2015的结果

Herzenstein et al 2024年的研究结果

可视化的方式 + 简单计算

下次实验的可重复性

离散变量

多次试验(多次进行重复实验)的成功率

人为分配的三种成功率(0.2, 0.5, 0.8)和它们出现的可能性

进行重复后的结果在三种成功率下出现的可能性

简单的手动计算

多次实验的可重复性

连续变量

无数次试验的成功率/正确率

进行重复后的结果在所有成功率/正确率下出现的可能性

进行重复后的结果在所有成功率/正确率下出现的可能性

已被证明的统计学公式

实验本身的可重复性

单一事件中体现出的贝叶斯公式#

  • 某个研究的可重复性与语言风格。

一项研究使用了确切语言（事件 B 已经发生）的心理学研究，其可重复的概率是多少？

  • A 事件代表的是一项心理学研究是可重复的

  • 事件代表的是一项心理学研究使用了确切语言

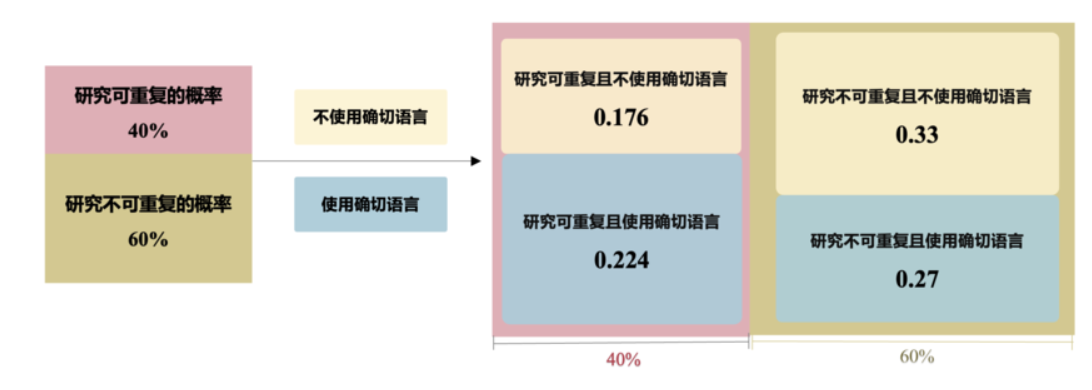
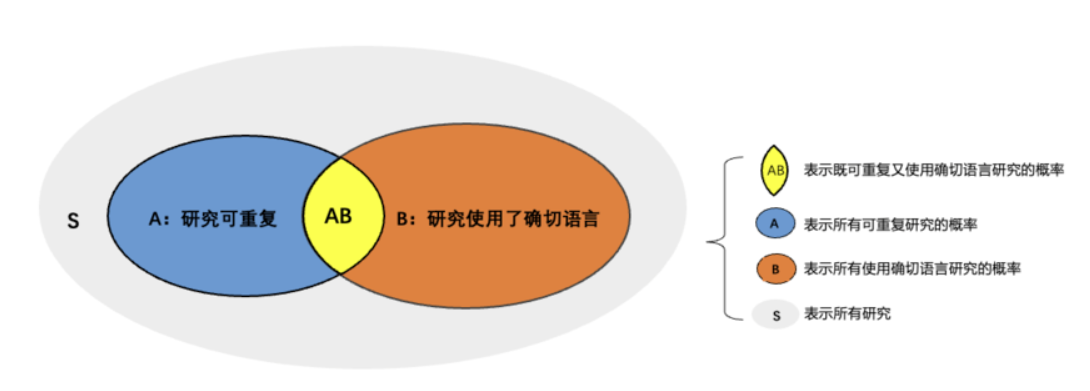
alt text

alt text

用条件概率公式表示：

\[ P(A|B) = \frac{P(A\bigcap B)}{P(B)} \]

其中，\(P(A\bigcap B)\)表示事件A和事件B同时发生的概率，即研究既是可重复的，又使用了确切语言，根据上图，这个值为0.224.

\(P(B)\)表示研究使用确切语言的总概率，表示为：

\[ P(B) = \frac{P(A\bigcap B)}{P(notA\bigcap B)} \]

即，可重复且使用确切语言的概率加上不可重复但使用确切语言的概率，具体为：

\[ P(B) = 0.224+0.27 = 0.494 \]

代入条件概率公式：

\[ P(A|B)=\frac{0.224}{0.494} ≈ 0.454 \]

结论

  • 条件概率告诉我们，随着我们获得新的信息（如事件 B 的发生）， 我们会调整关于在这种情况下事件 A 发生的概率\(P(A|B)\)

\[ P(A|B)=\frac{P(A\bigcap B)}{P(B)} \]

  • 这个公式就是鼎鼎大名的贝叶斯公式

  • 这正是贝叶斯定理的基础思想：我们通过结合先验信息和新观测数据，不断更新对事件发生概率的认识

随机变量随着信息的更新 –> 贝叶斯法则#

  • 贝叶斯公式描述的是，给定事件 B 已经发生的情况下，事件 A 的发生概率如何调整。

  • 假如这里的A是特定模型下的一个参数(随机变量)，关于A的概率分布来自于我们的先验知识\(P(A)\)

  • 假如这里的B是我们为了理解A的数据，根据我们模型和A的分布，可以计算似然\(P(B|A)\)

  • 经过贝叶斯更新，我们可以得到更新的关于A的概率分布：\(P(A|B)\)

上述过程中，我们从贝叶斯公式“升级”成了利用贝叶斯法则进行推断：

  • 贝叶斯推断的核心思想：在新数据的条件下，更新我们的信念。

  • 贝叶斯推断的特点：（不同的）先验与（不同的）数据之间平衡、序列性等

所以：

1、贝叶斯推断的本质与数数相似，符合人类的推理直觉。

2、贝叶斯统计的主要作用在于将这种直觉形式化，通过数学工具帮助我们在更复杂的情境中解决问题。

🤔因此，也引出一个问题：既然贝叶斯推断这么符合人的直觉，为什么我们以前在心理统计课上不教它呢？

  • 贝叶斯推断的核心在于后验分布。通过结合先验和似然，我们能够得到对未知参数的最新估计。

  • 贝叶斯推断的难点在于：如何得到后验分布？

Beta-Binomial是如何得到后验分布的？

先前例子：推断编号为 “82111” 被试的正确率，观测到的数据为253 次试验数据，其中有 152 次判断正确。

先验（Informative Prior），\(Beta(70,30)\)

–>后验分布可以通过简单的计算得到：

\[ \pi|(Y=152) \sim Beta(70+152,30+101) \]

虽然这种计算非常简洁，但问题在于：是不是所有的贝叶斯分析都如此简洁？

Beta-Binomial分布计算简便的原因为：它属于共轭分布簇

共轭先验 (Conjugate Prior)#

共轭先验：在贝叶斯推断中，在给定数据（似然函数）后，先验分布可以产生一个属于同一分布簇的后验分布，称该先验为共轭先验。

具体来说，给定一个概率分布簇和它的参数，如果这个参数的先验分布与后验分布属于同一个分布簇，那么这个先验分布被称为该似然函数的共轭分布。

共轭先验的优点是：

1、计算简便：共轭先验使得后验分布的数学形式保持简单，易于计算。

2、解释性：共轭先验有时可以提供直观的参数解释。

3、封闭形式的解决方案：使用共轭先验可以使得后验分布有封闭形式的解，这对于抽样和推断非常有用。

以正确率\(\pi\)为例，我们考虑以下情况：

  • \(\pi\)的先验分布的概率密度函数（PDF）为\(f(\pi)\)

  • 给定\(\pi\)下观测数据\(Y\)的似然函数为\(L(\pi|Y)\)的共轭先验

如果后验分布的PDF\(f(\pi|Y)\)与先验分布属于同一模型家族，并且可以表示为：

\[ f(\pi|Y) \propto f(\pi)·L(\pi|Y) \]

那么，这个先验分布\(f(\pi)\)就是似然函数\(L(\pi|Y)\)的共轭先验。

Beta-Binomial conjugate family

在lec3 与 lec4 中，我们使用了\(Beta\)分布来反映我们对参数\(\pi\)的先验认识。

我们知道若先验可以用\(Beta(\alpha,\beta)\) 描述，收集到的数据可以用\(Bin(n,\pi)\)描述，后验分布就可以用\(Beta(\alpha+y,\beta+n-y)\)描述。

非共轭先验会带来什么

让我们再回到随机点运动任务正确率的例子，考虑一个非共轭先验的状况

假如此时的先验分布\(f(\pi)\)不是\(Beta\)分布，而是以下形式：

\[ f(\pi)=e-e^{\pi} for~\pi \in [0,1] \]

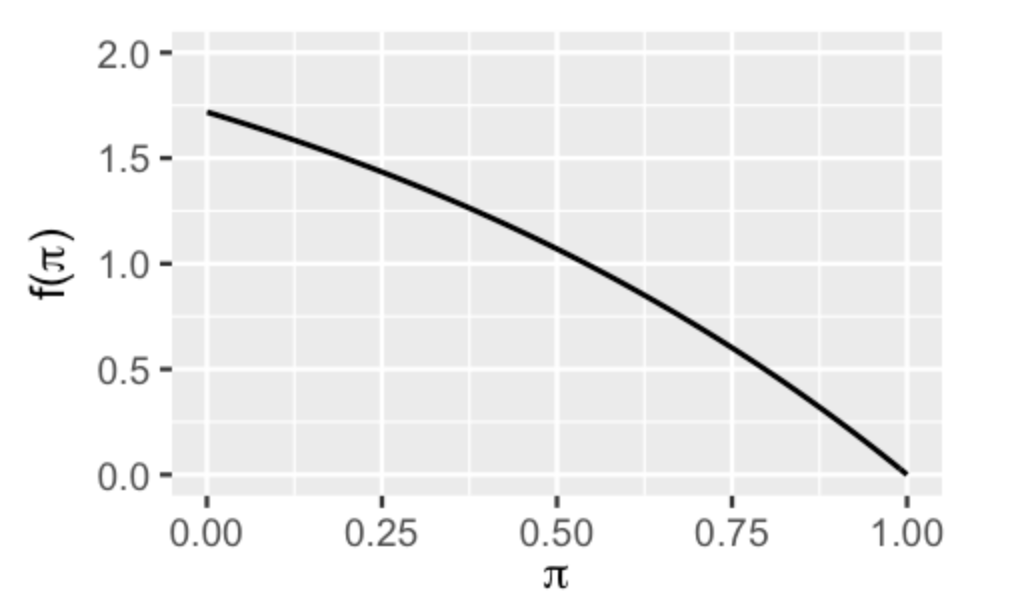
假设，数据为 50 次反应中有 10 次正确，那么在共轭先验\(Beta(45,55)\)的情况下，后验分布可以简洁地写为\(Beta(55=45+10,95=55+40)\)。但在共轭先验的情况下，该后验分布的结果变得很繁琐。并且在非共轭先验的情况下，我们很难从这个后验表达式中获得类似的直觉。

此时似然函数仍是一个二项分布

\[ L(\pi|y=10) = (^{50}_{10})\pi^{10}(1-\pi)^{40} for~\pi \in [0,1] \]

后验可以写成：

\[ f(\pi|y=10)\propto f(\pi)L(\pi|y=10) = (e-e^{\pi})·(^{50}_{10})\pi^{10}(1-\pi)^{40} \]

加入归一化常数后：

\[ f(\pi|y=10)=\frac{(e-e^{\pi})\pi^{10}(1-\pi)^{40}}{\int^1_0(e-e^{\pi})\pi^{10}(1-\pi)^{40}d\pi} for~\pi\in [0,1] \]

其他共轭先验

除了 Beta-Binomial 和 Normal-Normal，贝叶斯推断中还有其他重要的共轭先验组合：

alt text

这些共轭家族的主要优势在于，极大简化了计算。

然而，在实际应用中，许多复杂的统计模型并没有简单的共轭先验。对于这些模型，计算后验分布中的分母（归一化常数）变得非常困难，甚至无法通过解析方式计算出来，如之前提到的 Beta-Binomial 在非共轭先验下的后验公式推导。

因此，贝叶斯推断在很长一段时期内，被困在共轭分布的范围内，导致其相对频率主义统计而言毫无优势可言。

但是计算机的出现改变了这一状况，基于数值的方法和近似的方法也能够在非共轭情况下获得后验分布，完成贝叶斯推断，这是现代贝叶斯统计获得广泛应用的前提。

Note:在本课中，我们不对共轭先验进行进一步介绍，如果想深入了解上述内容，可访问我们去年lecture 5 的 jupyter notebook以及本课件最后的附录。

在实际应用中，我们会遇到一些问题，比如：

  • 对于连续变量，在计算边缘似然\(f(y)\)时需要积分，然而某些情况下(例如，先验不是似然的共轭分布)，此时积分难以或无法计算。

  • 当参数或数据维度较高时，计算边缘似然\(f(y)\)的难度会变得非常困难。

条件概率的计算

最初，当我们只有一个或少数几个参数时，条件概率的计算相对简单。例如，给定数据\(y\)，参数\(θ_k\)的条件概率可以表示为：

\[ f(θ_k|y)=\frac{f(θ_k)L(θ_k|y)}{f(y)} \]

  • 这里，\(f(θ_k)\)是参数\(θ_k\)的先验概率分布

  • \(L(θ_k|y)\)是似然函数，而\(f(y)\)是数据的边缘似然

连续变量的挑战

当参数\(θ_k\)是连续变量时，计算开始变得复杂。我们需要对\(θ_k\)的所有可能值进行积分来计算边缘似然\(f(y)\)：

\[ f(y)=\int f(θ_k)L(θ_k|y)dθ_k \]

  • 这个积分可能已经比较难以计算，特别是当似然函数\(L(θ_k|y)\)的形式复杂时。

多个连续变量的复杂性

当模型包含多个连续参数\(θ_1,θ_2,....,θ_k\)时，计算边缘似然\(f(y)\)的分母变得更加复杂：

挑战在于：

  • 计算量增加：随着参数数量的增加，多变量积分的计算量呈指数级增长。

  • 解析解难以获得：对于某些复杂的似然函数，可能不存在封闭形式的解析解，使得传统的积分方法无法直接应用。

  • 数值积分的限制：即使使用数值积分方法，也可能因为维度灾难（curse of dimensionality）而面临计算上的困难，导致精度下降或计算成本过高。

对后验的近似(Approximating the Posterior)#

“计算机的出现改变了这一状况，基于数值的方法和近似的方法也能够在非共轭情况下获得后验分布，完成贝叶斯推断，这是现代贝叶斯统计获得广泛应用的前提。”

在解决计算问题时，现代方法主要分为两大类：数值方法和近似方法。

  • 数值方法通过精确的算法直接求解问题，包括迭代法、分解法等。

  • 而近似方法则通过牺牲一定的精度来换取计算效率，包括蒙特卡洛模拟、变分法、插值与拟合技术等。

接下来，我们将介绍两种近似方法：

1、网络近似

2、马尔可夫链蒙特卡洛（MCMC）

Contents