Metropolis-Hastings(MH)算法#
在刚才的例子中,我们已经涉及到 MH 算法最朴素的思想:
后验分布模型可以通过公式进行推导得到,然而无法对它进行直接采样。
我们可以根据后验模型 y 轴的大小来决定 x 轴参数的数量。
例如,我们均匀的从参数的范围(x~[0,1])中抽取10000个参数样本\(\mu_i\),然后我们计算对于每个\(\mu_i\)的\(f(\mu_i)\)的大小,\(f(\mu_i)\)越大那么\(\mu_i\)被保留的可能性越高。
正如之前提到,计算\(f(\mu_i)\)是比较困难的,我们可以计算非标准化的\(f(\mu_i)\)。
此外,直接在[0,1]中均匀的采样效率太低,我们在接下来会利用 MCMC 状态转移的性质来提高采样效率。
接下来,我们来体验一下这个奇妙的过程:
建议分布(proposed distribution)#
为了提高采样效率,我们不会直接从一个分布中进行大量采样,再进行筛选(也被称为拒绝),这种方式在复杂分布中效率非常低。
也就是说,如何根据当前的采样值,去propose下一次采样的值?
因此在 MCMC 中,我们会构造一个建议分布 (proposed distribution)\(q(x)\),然后利用 MCMC 状态转移的性质来进行采样。
通过建议分布,我们可以在 MCMC 的状态转移过程中构造出一条马尔可夫链。这条链最终会收敛于目标后验分布,使得生成的样本接近真实的目标分布。
在刚才所讲的心情状态的变化过程实际上就是一个建议分布的例子。
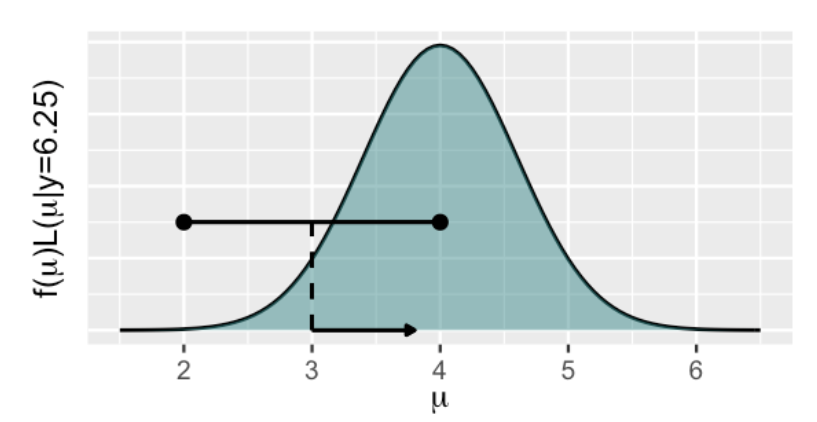
举例:我们随机选取了一个起点3,然后以3为中心进行propose,比如对3-1或3+1进行下一次的选取,这个时候就涉及一个问题,我们对下一次采样的接受策略是如何的?
接受率(acceptance probability)#
虽然我们了解了当前样本可以根据上一次的样本从建议分布中进行采样\(\theta^n \sim Normal(\theta_k^{n-1},\sigma)\)。
然而,我们如何判断这个采样是否合理呢?换句话说,我们需要思考是否保留或拒绝这个采样。
现在,我们来看一下不同的接受策略会导致什么样的情况
不同接受策略的影响#
我们可以考虑三种接受建议的情况:
1:始终不接受提议。————Tour2,采样值始终不变,一直停留在同一个值
2:始终接受提议。————Tour3,完全是随机的,采样不会稳定在某一个范围
3:只有当提议(n+1)的后验可能性大于当前(n)值的后验可能性时,才接受提议 。————Tour1,逐渐收敛到一个稳定的值,但采样只停留在\(\mu=4\)附近
我们来看一下三种情况对应生成的trace plot:
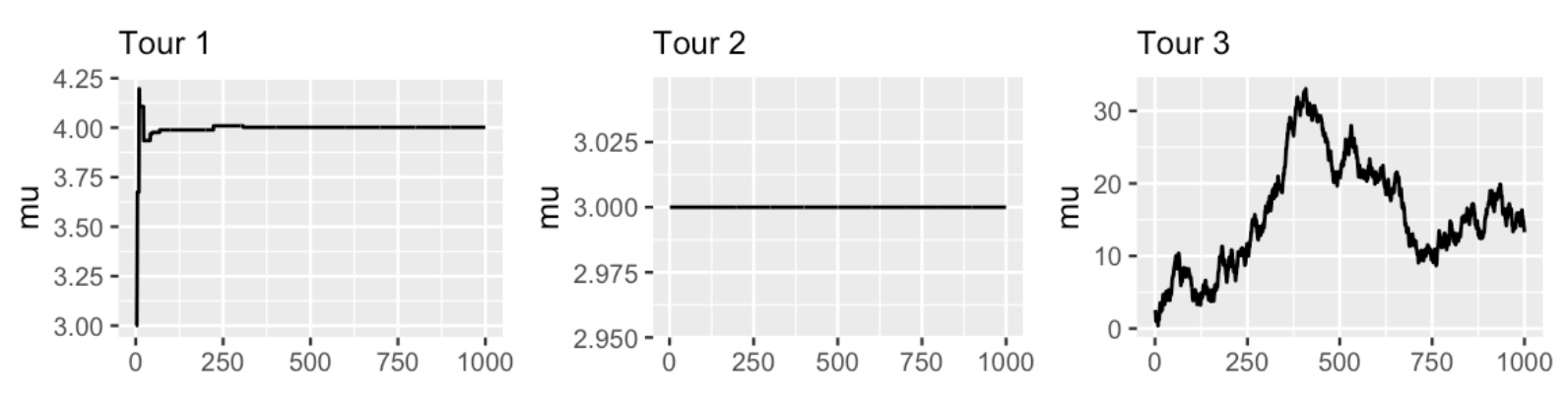
虽然Tour3看起来比前两种更靠谱,但是会产生一个问题:采样只停留在一个固定的值上面,而不会取到其他的值。
因此,这三种策略都不是很合适。
接受率(acceptance probability)
可见,选择一个合适的接受策略非常重要。而接受率 (\(\alpha\), acceptance probability)就是为了解决这个问题。
首先,我们将从建议模型中抽取一个新的参数\(\theta^{n+1}\)的概率为\(q^{(\theta^{n+1}|\theta^n)}\)
对于是否接受\(\theta^{n+1}\),我们定义接受概率\(\alpha\)
别看这公式很复杂,其实很简单:
数的上下分别代表下一个参数\(\theta^{n+1}\)和当前参数\(\theta^n\)的非标准化后验。即我们之前提到,要通过非标准化后验来判断是否接受一个参数。
其中,\(f(\theta)L(\theta|y)\)为非标准化后验
\(q(\theta^n|\theta^{n+1})\)部分代表了从建议分布中采样新参数的过程。
可以想象,\(\frac{f(\theta^{n+1})L(\theta^{n+1}|y)}{f(\theta^n)L(\theta^n|y)}\)大于1且其值越大,表明下一个参数\(\theta^{n+1}\)的后验概率越大,因此它越有可能被接受。
如果\(\frac{f(\theta^{n+1})L(\theta^{n+1}|y)}{f(\theta^n)L(\theta^n|y)}\)小于1,则代表下一个参数\(\theta^{n+1}\)的后验概率过小,因此我们要舍弃它。
所以,对于是否接受或拒绝新的参数\(\theta^{n+1}\),则有:
也就是如果我们不接受新的参数,那我们用原来的参数替代现在的参数。
这样避免了参数采样被浪费,并且使得概率更大的参数被更多的采样。
总的来说,MH 算法包含两个关键思想和两个关键步骤:
两个关键思想
1.根据非标准化的后验进行参数的接受或拒绝
2.根据 MCMC 的特性设置建议分布来完成状态转移
两个关键步骤
1.设定建议分布
2.根据建议分布的参数、未标准化后验计算接受率
代码演示#
import numpy as np
import scipy.stats as st
import pandas as pd
import seaborn as sns
首先,我们假设当前的参数值\(\theta^n=3\),然后我们根据该参数设定建议分布,并进行一次新的采样。
注意,为了方便演示,我们将建议分布(正态分布)的\(\sigma\)固定为1。
#设置随机种子,以便重复
np.random.seed(2024)
current = 3 # 假设theta(n)为3
proposal = st.norm(current, 1).rvs() # 从当前正态分布(均值为current,标准差为1)中抽出一个样本,rvs()默认只抽取1个样本值
print("从建议分布中新采样 θ(n+1)为:",proposal)
输出:从建议分布中新采样 θ(n+1)为: 4.668047321311954
接着,我们根据新采样得到的参数计算其相关的接受率。
注意,我们假设先验正态分布的参数为:mean = 3, sigma = 1
另外,我们假设似然模型仅包含一个数据:Y = 6
# 设置先验
prior = st.norm(loc = 3, scale = 1)
def likelihood(theta):
Y = 6 # 假设数据 Y 为 6
return st.norm(loc = theta, scale = 0.75).pdf(Y) # 注意:这里为方便演示固定 scale = 0.75
# 计算建议位置(n+1)的未归一化的后验概率值(先验*似然)
proposal_posterior = prior.pdf(proposal) * likelihood(proposal)
# 计算当前位置(n)的未归一化的后验概率值(先验*似然)
current_posterior = prior.pdf(current) * likelihood(current)
# 计算接受概率α,为两者概率值之比
alpha = min(1,proposal_posterior/current_posterior)
# 打印出接受概率α
print("后验比为:", proposal_posterior/current_posterior, ", alpha为:", alpha)
后验比为: 153.2136146465854 , alpha为: 1
我们根据接受率\(\alpha\)来决定是否接受建议分布的参数作为新的采样值。
# 根据接受概率α进行抽样,抽样内容为建议位置和当前位置
next_stop = np.random.choice([proposal, current], 1, p=[alpha,1-alpha])
# 打印出下一个位置的值
next_stop[0]
#从第一段代码我们可以看到此时的接受概率α=1,因此接受了建议值作为我们的下一个值
输出:4.668047321311954
上面就是MH算法的一次迭代演示。
定义单次采样函数
我们可以直接定义一个函数,将刚刚的操作全都结合在一起,这样当我们想进行抽样的时候,不用重复写代码。
proposal |
alpha |
next_stop |
|
|---|---|---|---|
0 |
3.091205 |
1 |
3.091205 |
# 变换不同的随机数种子,其实也是生成不同的建议值
np.random.seed(83)
one_mh_iteration(current=3)
proposal |
alpha |
next_stop |
|
|---|---|---|---|
0 |
3.849313 |
1 |
3.849313 |
多次采样
上述函数只进行了一次采样,即当前位置为3时,下一个可能采样的结果
基于当前位置,提出下一个采样值,接受或拒绝它。那么新的采样值就变成了当前位置,我们需要不断重复这个过程
def mh_tour(N, w = 1):
"""
N为迭代次数,w为均匀分布的一半宽度
我们在单次采样函数的基础上叠加了一个循环
将每次的采样结果存在mu[i]中,
在每次采样结束后,将采样结果替换为当前位置
返回值为迭代次数,和每次采样得到的结果
"""
current = 3
mu = np.zeros(N)
for i in range(N):
sim = one_mh_iteration(current,sigma)
mu[i] = sim["next_stop"][0]
current = sim["next_stop"][0]
return pd.DataFrame({"iteration": range(1,N+1), # range(start,end) 这里对应1,N+1,才会使得iteration数列从1开始,便于理解
'mu': mu})
# 调用定义好的函数,将采样次数设为5000,均匀分布的一半宽度设为1
np.random.seed(84735)
mh_simulation = mh_tour(N=5000)
mh_simulation.tail() #.tail()为查看结果的最后几行,()默认为5行
iteration |
mu |
|
|---|---|---|
4995 |
4996 |
4.528634 |
4996 |
4997 |
4.528634 |
4997 |
4998 |
4.745413 |
4998 |
4999 |
5.847077 |
4999 |
5000 |
5.847077 |
采样结果图示
import matplotlib.pyplot as plt
#生成一行两列的画布
fig, axs = plt.subplots(1, 2, figsize=(20, 5))
#density plot:在第一列绘制出采样结果的分布
axs[0].hist(mh_simulation["mu"],
edgecolor = "white",
color="grey",
alpha = 0.7,
bins = 20,
density = True)
axs[0].set_xlabel("mu", fontsize=16)
axs[0].set_ylabel("density", fontsize=16)
# 绘制分布外围线条
x_norm = np.linspace(2,10,10000)
y_norm = st.norm.pdf(x_norm, loc=mh_simulation["mu"].mean(), scale=mh_simulation["mu"].std())
axs[0].plot(x_norm, y_norm, color='blue')
#trace plot:在第二列绘制出每一次的采样结果
axs[1].plot(mh_simulation["iteration"], mh_simulation["mu"],
color="grey",)
axs[1].set_xlabel("iteration", fontsize=16)
axs[1].set_ylabel("mu", fontsize=16)
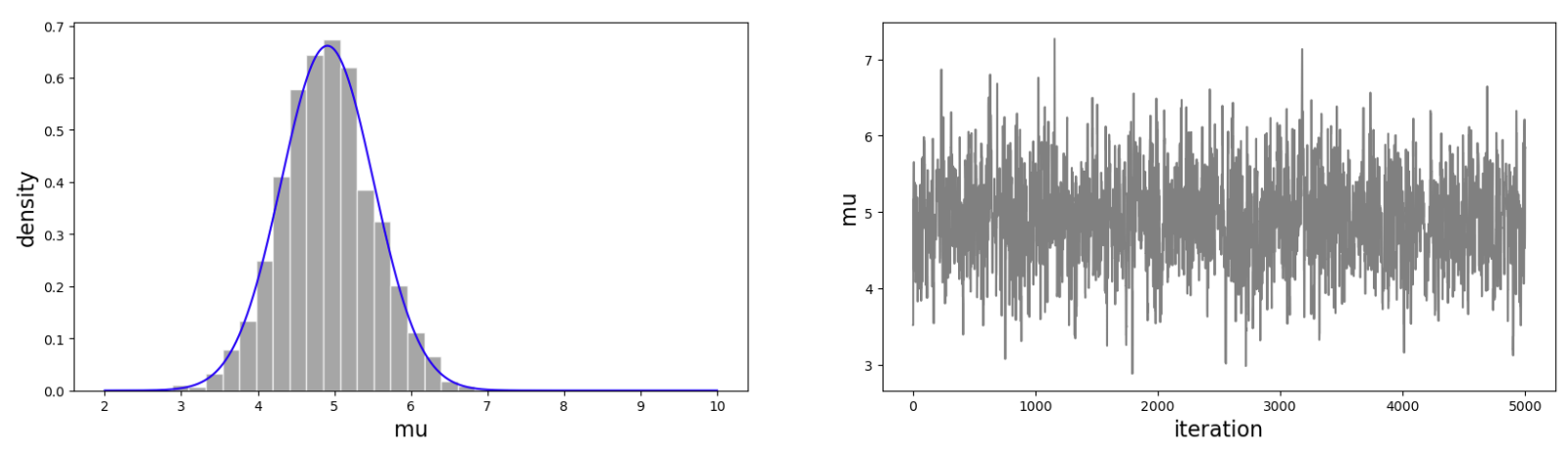
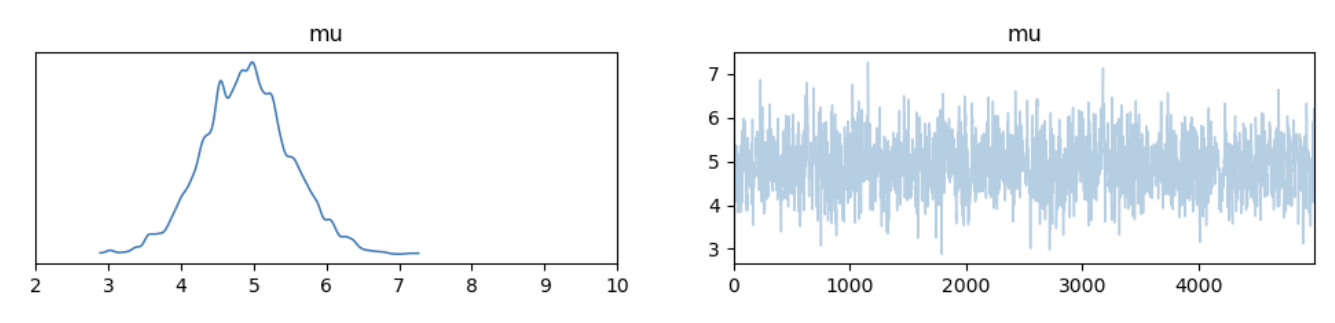
我们可以使用 arviz 简化这个绘图的过程
import arviz as az
import matplotlib.pyplot as plt
ax = az.plot_trace({"mu":mh_simulation["mu"]})
ax[0, 0].set_xlim(2, 10)
调试(Tuning)Metropolis-Hastings 算法#
在建议分布\(\mu_{n+1}|\mu_n \sim Normal(\mu_n,\sigma)\)中,\(\sigma\)反映了建议选项的分布宽度,对它的选择也会影响马尔科夫链的表现
🤔我们还是使用MH算法,请你判断三种不同的\(\sigma\)分别对应下面的哪些轨迹图和密度图?
\(\sigma\)=0.01
\(\sigma=1\)
\(\sigma\)=100
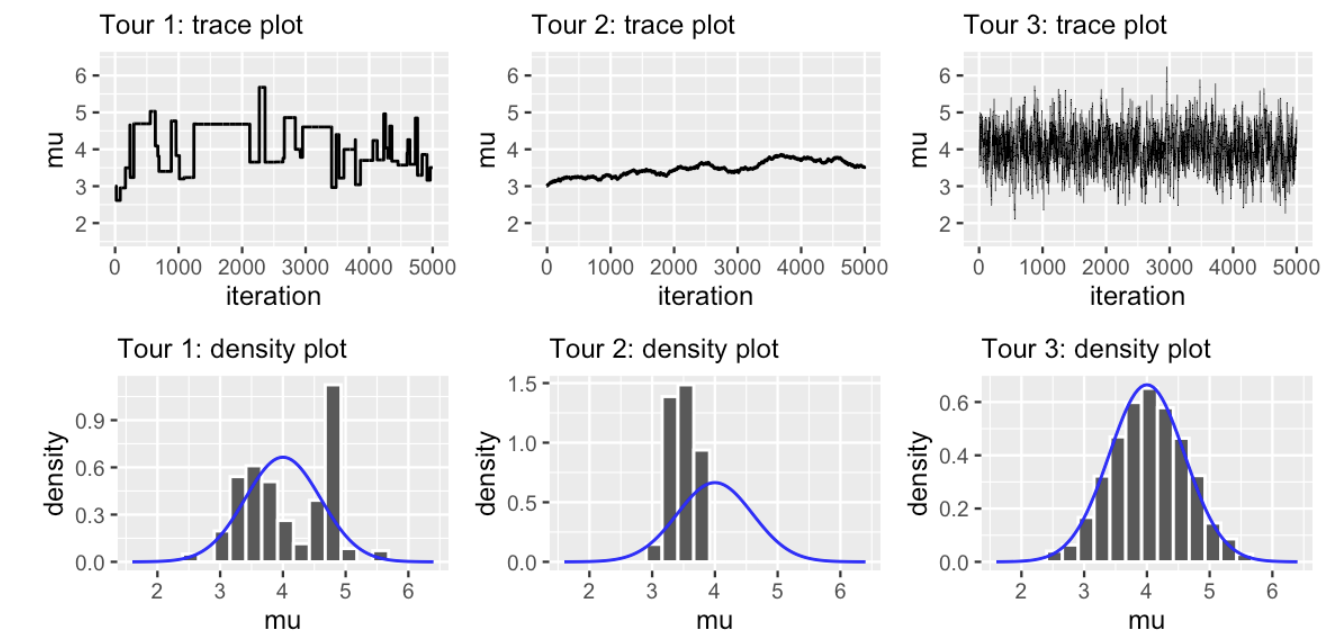
可以结合以下代码进行判断:
import numpy as np
import matplotlib.pyplot as plt
import arviz as az
import scipy.stats as st
import pandas as pd
def one_mh_iteration(current, sigma = 1):
"""
def后面为函数值,current为输入值,作为建议分布(正态分布)的均值
接下来的代码和之前一样
return 则是该函数返回的值,我们将建议值,接受概率,和下一个位置这三个值组成了一个数据框进行返回
"""
proposal = st.norm(current, sigma).rvs()
prior = st.norm(loc = 3, scale = 1)
def likelihood(theta):
# 假设数据 Y 为 6
Y = 6
return st.norm(loc = theta, scale = 0.75).pdf(Y)
proposal_posterior = prior.pdf(proposal) * likelihood(proposal)
current_posterior = prior.pdf(current) * likelihood(current)
alpha = min(1,proposal_posterior/current_posterior)
next_stop = np.random.choice([proposal, current], 1, p=[alpha,1-alpha])
return pd.DataFrame({"proposal":[proposal],
"alpha":[alpha],
"next_stop":[next_stop[0]]})
def mh_tour(N, sigma = 1):
"""
N为迭代次数,sigma为正态建议分布的标准差
我们在单次采样函数的基础上叠加了一个循环
将每次的采样结果存在mu[i]中,
在每次采样结束后,将采样结果替换为当前位置
返回值为迭代次数,和每次采样得到的结果
"""
current = 3
mu = np.zeros(N)
for i in range(N):
sim = one_mh_iteration(current,sigma)
mu[i] = sim["next_stop"][0]
current = sim["next_stop"][0]
return pd.DataFrame({"iteration": range(1,N+1),
'mu': mu})
#===========================================================================
# 请修改 ... 中的值。
#===========================================================================
np.random.seed(84735)
mh_simulation = mh_tour(N=5000, sigma= ...)
az.plot_trace({"mu": mh_simulation["mu"]})
#===========================================================================
# 可以自行复制代码多试几次
#===========================================================================
mh_simulation = mh_tour(N=5000, sigma= ...)
az.plot_trace({"mu": mh_simulation["mu"]})
总结
当\(\sigma\)=0.01时:
建议分布的范围很窄,比如\(Normal(3,0.001)\),这会导致下一个建议值和当前值非常接近,则\(f(\mu')L(\mu'|y)≈f(\mu)L(\mu|y)\)
那么我们很容易接受下一个采样值,但尽管马尔科夫链一直在转移,但探索的范围太窄了,我们可以看到采样一直在3附近
当\(\sigma=100\)时:
类似的,我们可以推知此时建议分布的范围太宽了,超出了\(\mu\)可能的取值
下一个建议值和当前值间隔太远,这会导致我们经常拒绝下一个采样值,多次停在当前位置。
最后,推荐 MCMC 讲解最好的视频(没有之一):【蒙特卡洛(Monte Carlo, MCMC)方法的原理和应用】 https://www.bilibili.com/video/BV17D4y1o7J2/?share_source=copy_web&vd_source=4b5b4646c3f53f1b80954c381226c913
如果还是不懂 MCMC 原理,那放弃也行…..
不了解 MCMC 原理,并不影响对于它的使用。
小结
无论是在这些相对简单的单参数模型设置中,还是在更复杂的模型设置中,Metropolis-Hastings 算法都是通过两步之间的迭代,从后验中产生近似样本:
设定建议分布
根据建议分布的参数、未标准化后验计算接受率
本节课我们只考虑了一种 MCMC 算法,即 Metropolis-Hastings。这种算法虽然功能强大,但也有其局限性。
在以后的章节中,我们的贝叶斯模型将增加大量参数。调整 Metropolis-Hastings 算法以充分探索每个参数会变得很笨重。
然而,即使 Metropolis-Hastings 算法的实用性达到了极限,它仍然是一套更灵活的 MCMC 工具的基础,包括自适应 Metropolis-Hastings、Gibbs 和 Hamiltonian Monte Carlo (HMC) 算法。其中,HMC 是 pymc 默认使用的算法。
