Different priors, different posteriors

Different priors, different posteriors#

不同先验分布对于后验的影响#

上节课，我们根据心理物理函数设置了不同的先验。

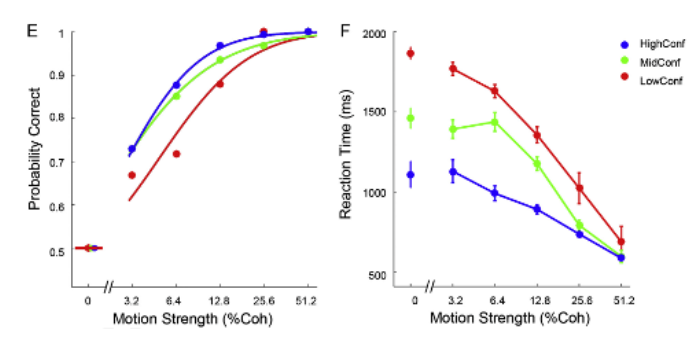
Shooshtari, S. V., Sadrabadi, J. E., Azizi, Z., & Ebrahimpour, R. (2018). Confidence representation of perceptual decision by EEG and eye data in a random dot motion task. Neuroscience, 406, 510–527. https://doi.org/10.1016/j.neuroscience.2019.03.031

然而，根据不同的研究或者理论，先验的设置也可能存在不同。

  • 本节课我们考虑如下三种不同的先验分布：

1、第一种先验和上节课相同，认为参数值\(π\)(正确率)在 0.7 左右，用 Beta(70,30)表示。

2、第二种先验比较极端，认为参数值\(π\)(正确率)大于 0.6，并且其值越大约有可能，用 Beta(10,1)表示。

3、最后一种“躺平”的思路认为，参数在\(π\) 0-1 之间出现的可能性是完全相同的，即先验可以用均匀分布表示Beta(1,1)。

现在，我们对这三种不同的先验进行可视化：

# 导入必要的库
import scipy.stats as st
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import preliz as pz

# 为 preliz 绘图设置图形样式
pz.style.library["preliz-doc"]["figure.dpi"] = 100
pz.style.library["preliz-doc"]["figure.figsize"] = (10, 4)
pz.style.use("preliz-doc")

# 创建一个1x3的网格子图
fig, axs = plt.subplots(1, 3)

# 绘制 Beta分布的PDF，并显示置信区间
pz.Beta(30, 70).plot_pdf(pointinterval=True, ax=axs[0], legend="title")
pz.Beta(10, 1).plot_pdf(pointinterval=True, ax=axs[1], legend="title")
pz.Beta(1, 1).plot_pdf(pointinterval=True, ax=axs[2], legend="title")

# 设置每个子图的X轴范围为0到1
for ax in axs:
    ax.set_xlim(0, 1)

# 显示绘制的图形
plt.show()

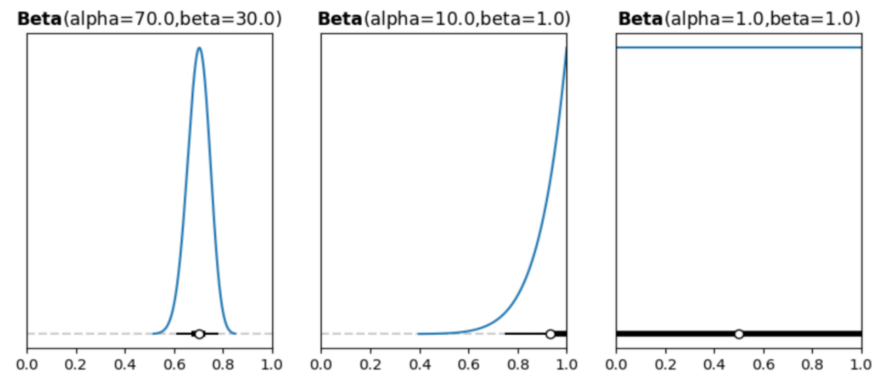
  • 先验从哪里来： 先验实际上本身蕴含了一定的信息，比如我们对某一事件的经验，或者是我们的一些常识，再或者我们先前看到的一些知识，最终形成了一个先验。

🤔思考：

  反观图右，这种先验信念反映了目前没有任何信息，因此假设所有可能性都是完全均匀的，但是这种均匀分布有时候是否不合理呢？

👉一个有趣的例子：

  假设我们在南师大的校门口记录路人的性别，那么最后在所有记录的路人中，男性路人的可能性是多少？

  首先，这个先验应当是一个二项分布（因为路人的性别要么是男要么是女），那么此时的先验还会是0到1之间的均匀分布吗？现在来看，0到1之间的均匀分布似乎不是一个合理的先验，因为我们具备的常识告诉我们，先验分布在0.5的附近更集中，似乎比0到1之间均匀分布更加的合理。

  • 因此，有时候我们可能觉得这种均匀分布看似很客观，但有时候并不能反映出一个合理的、符合常识的先验。

不同类型的先验#

我们来回顾一下先验中我们可以获得什么信息：

  • 在上图中，不同的先验，反映了研究者对正确率的不同信念(认为\(π\)主要集中分布在哪里)

  • 同时，先验分布的集中程度也反映了人们对某种信念的肯定程度

🤔举例：

  • 对于\(Beta(10,1)\)这个先验，\(π\)的取值集中分布在0.6-1.0这种“高正确率区域”，说明研究者对研究的正确率的信念是很肯定的。

  • 而对于\(Beta(1,1)\)这个先验，\(π\)的取值均匀分布在0-1之间，研究者觉得\(π\)取任何值的可能性都是一样的，换言之他们也不知道\(π\)可能是多少。

以上两种先验，可被总结为信息型先验(informative prior) 和 模糊型先验(vague prior) ，其中：

信息型先验#

  • 先验分布较窄，取值范围小。

  • 代表研究者对研究的正确率有强烈且确定的信念。

模糊型先验#

  • 先验分布较宽，取值范围大。

  • 代表研究者对研究的正确率缺乏确定的信念。

结合数据查看先验对于后验的影响#

在继续探究不同的先验如何影响后验之前，我们还需要一些数据

这里以Evans et al.（2020, Exp. 1） 的数据为例：

Evans, N. J., Hawkins, G. E., & Brown, S. D. (2020). The role of passing time in decision-making. Journal of Experimental Psychology: Learning, Memory, and Cognition, 46(2), 316–326. https://doi.org/10.1037/xlm0000725

try:
  data = pd.read_csv("/home/mw/input/bayes3797/evans2020JExpPsycholLearn_exp1_full_data.csv")
except:
  data = pd.read_csv('data/evans2020JExpPsycholLearn_exp1_full_data.csv')

# 选取需要的列
data = data[["subject", "percentCoherence", "correct", "RT"]]

# 筛选符合条件的数据
data_subj1 = data.query('subject == 82111 & percentCoherence == 5')

#统计 'binary' 列中各个值的出现次数
print(data_subj1['correct'].value_counts())
data_subj1.head(5)

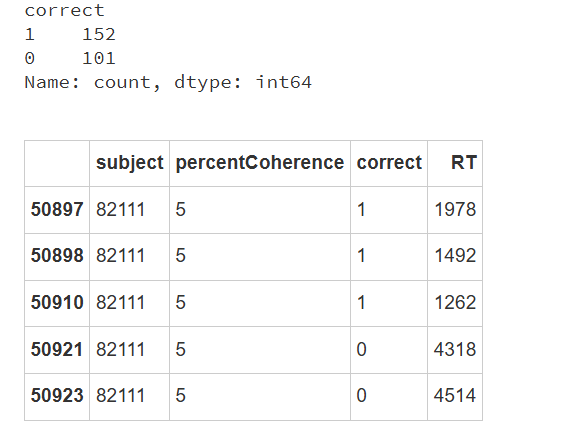
绘制三种先验-似然组合：

# 定义不同的 Beta 分布参数
params = [(70, 30), (10, 1), (1, 1)]

fig, axes = plt.subplots(nrows=1, ncols=len(params), figsize=(15, 4))

# 循环遍历不同的参数组合
for (alpha_, beta_),ax in zip(params, axes.flatten()):
   
    bayesian_analysis_plot(alpha=alpha_, beta=beta_, y=152, n=253, ax=ax, plot_posterior=False)
    
    # 设置子图标题
    ax.set_title(f'prior: Beta({alpha_},{beta_})')

# 移除图的上、右边框线
sns.despine()

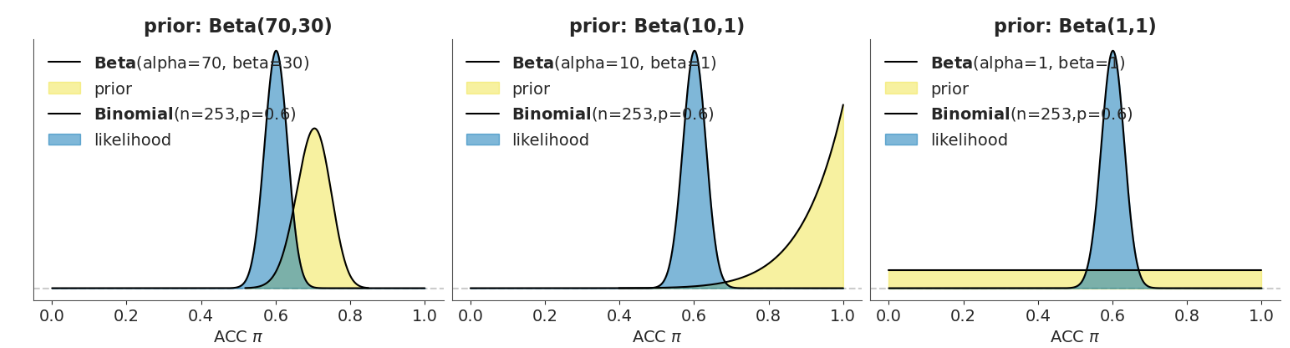
alt text

🤔思考时间

根据这三种先验-似然组合，猜测一下后验分布的形状？

后验图示#

我们可以使用公式来快速得到三种后验的表达式：

\[ \pi|(Y=y)\sim Beta(\alpha+y, \beta+n-y) \]

Analyst

Prior

Posterior

\(\alpha\)

Beta(70,30)

Beta(222,131)

\(\beta\)

Beta(10,1)

Beta(162,102)

mean

Beta(1,1)

Beta(153,102)

在表格中，每一行展示了不同被试的先验分布和后验分布。通过结合先验和观测数据，我们得到了相应的后验 Beta 分布。

接下来，我们可以将这些分布可视化，绘制出三种后验分布的图示，以便直观展示更新后的正确率\(\pi\)分布。

# 定义不同的 Beta 分布参数
params = [(70, 30), (10, 1), (1, 1)]

fig, axes = plt.subplots(nrows=1, ncols=len(params), figsize=(15, 4))

# 循环遍历不同的参数组合
for (alpha_, beta_),ax in zip(params, axes.flatten()):
   
    bayesian_analysis_plot(alpha=alpha_, beta=beta_, y=152, n=253, ax=ax)
    
    # 设置子图标题
    ax.set_title(f'prior: Beta({alpha_},{beta_})')

# 移除图的上、右边框线
sns.despine()

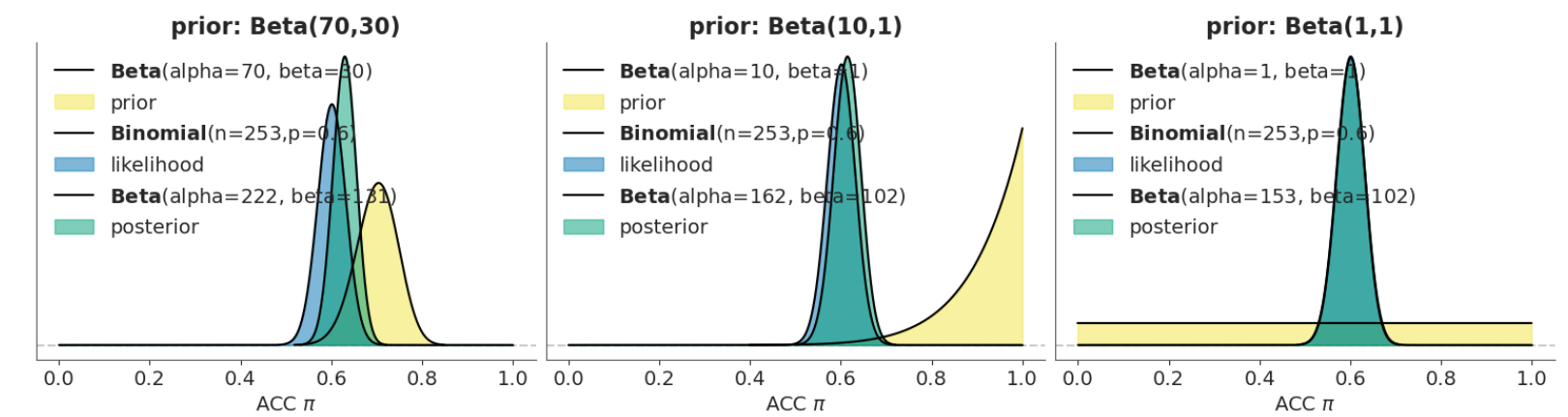
alt text

😊根据我们的直觉观察，先验对后验的影响较小，而似然对后验的影响似乎更大，因为后验分布更偏向于likelihood。例如最右边这幅图，在先验为0-1的均匀分布的情况下，后验和似然几乎是重叠的。

两种先验模式下的后验#

  1. 模糊型先验下：

  • 如果研究者对正确率没有明确预期，后验分布几乎完全由数据（似然分布）决定。由于模糊型先验（如\(Beta(1,1)\)）不提供关于\(π\)的有效信息，后验与似然分布几乎重合。

  1. 信息型先验下：

  • 当研究者对正确率有较强的信念，后验分布依然会受到先验的显著影响。例如，使用\(Beta(10,1)\)作为信息型先验，后验分布会集中在0.6-0.8区域，反映了研究者对\(\pi\)的较高信心。

  1. 总结：

  • 模糊型先验：后验主要由数据决定。

  • 信息型先验：先验对后验有强影响，后验分布倾向于维持先验的形状。

极端先验#

  在贝叶斯分析中，虽然我们通常讨论有信息和无信息的先验，但有时先验选择可能会导致严重的偏离。极端固执的先验模型可能会使贝叶斯方法失去其序列分析的优势。

  • 这种极端先验模型通常包含先验概率为零的信念。

  • 例如，研究者可能对随机点运动任务的正确率持有固执的观点，坚信其正确率较低。他们可能认为\(π\)的任何值在 0 到 0.25 之间都是等可能的，并坚决认为其不会超过 0.25。为了表达这种先验信念，可以采用 0 到 0.25 之间的均匀模型（uniform model）。

\[ \pi \sim Unif(0,0.25) \]
\[ f(\pi)=4~~for~\pi \in [0,0.25] \]

现在，假设做完实验后发现正确率为80%，这个80%的数据与实验者的信念相悖。

🤔思考：

根据先验和数据，猜测下面哪副图更符合随机点运动任务正确率的后验分布？

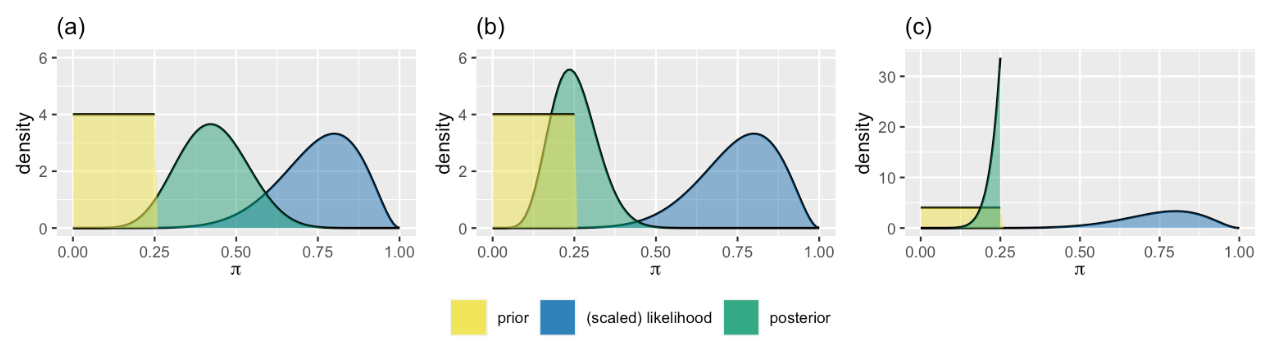
alt text

  根据我们的直觉来看，图 (c)似乎更符合后验分布，尽管图 (c)看起来奇怪， 但它的确代表了实验者在观察到数据的情况下对正确率\(π\)的更新。并且我们在图中可以看出：

无论收集到多少信息，后验概率永远不会超过0.25这个上限，此时先验已经完全约束住了后验。

  • 也就是说，如果我们的先验设计的非常不合理，那么无论我们收集到多少数据，后验概率都不会更新到正确的区域。

此外，还有一种情况是，对于有信息的先验，如果过于偏向某一特定值，也可能导致极端先验的出现：

  • 例如，同样对于先验是 0.7 的情况，如果先验过于有“信息”，那么数据可能对后验不产生或产生较小的影响。

# 定义不同的 Beta 分布参数
params = [(70, 30), (700, 300), (7000, 3000)]

fig, axes = plt.subplots(nrows=1, ncols=len(params), figsize=(15, 4))

# 循环遍历不同的参数组合
for (alpha_, beta_),ax in zip(params, axes.flatten()):
   
    bayesian_analysis_plot(alpha=alpha_, beta=beta_, y=152, n=253, ax=ax)
    
    # 设置子图标题
    ax.set_title(f'prior: Beta({alpha_},{beta_})')

# 移除图的上、右边框线
sns.despine()

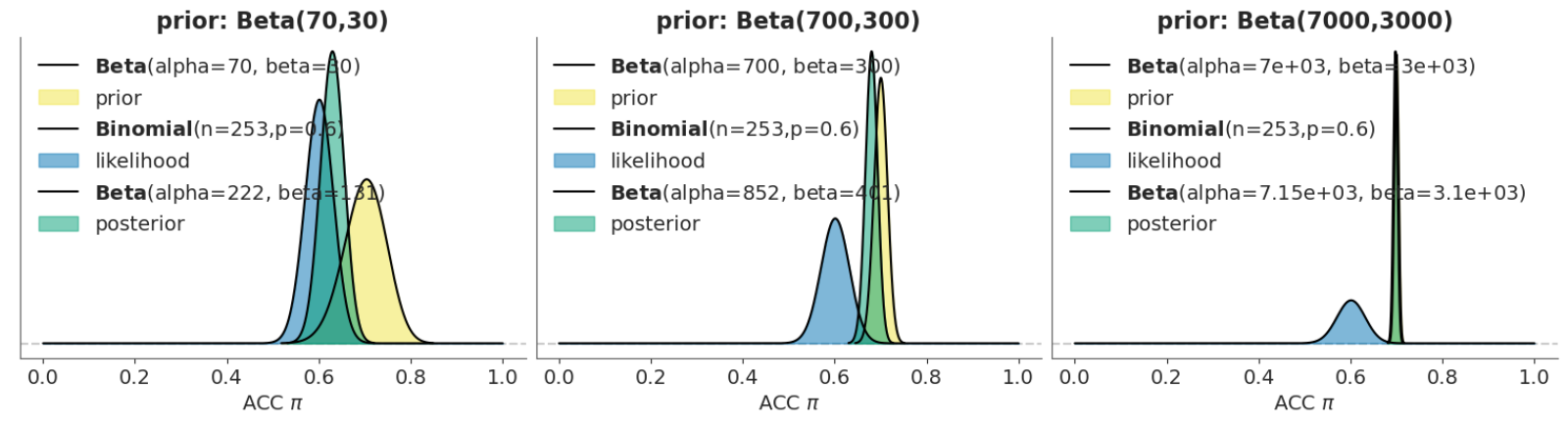
alt text

  从左到右可以明显看出，随着先验分布（黄色）越来越极端，数据（蓝色）对先验更新的能力会越来越弱。当先验非常极端时（Beta(7000,3000)），后验与先验几乎重叠，此时我们的数据几何没有办法去更新这个先验。

Tips：如何避免令人遗憾的先验模型

  • 幸运的是，我们有一些好消息, 这种使得贝叶斯序列分析失效的情况是完全可以避免的。

  • 确保对每个可能的\(\pi\)值都分配非零的可信度，即使这个可信度接近于零。例如，如果\(\pi\)是一个可以从 0 到 1 的比例，那么你的先验模型也应该在这个连续范围内进行定义

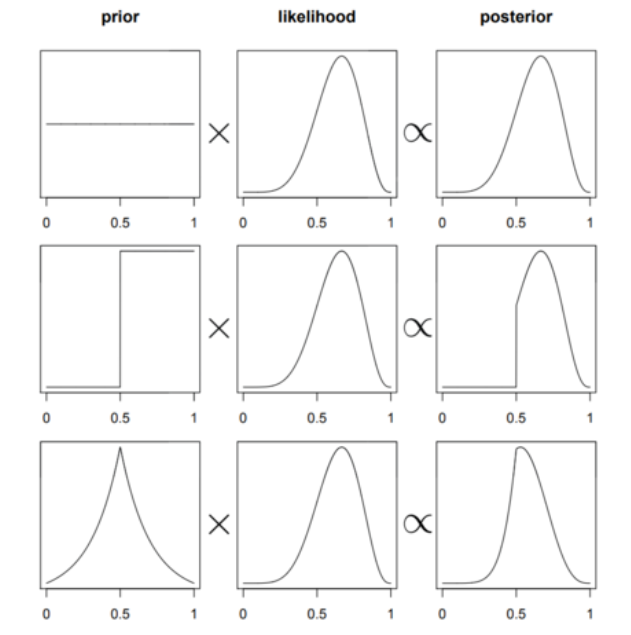
通过上面的图可以看出，在数据或似然相同的情况下，不同的先验分布会产生不同的后验分布。

🤔思考：当其他研究者询问：你为什么要用这个先验？这个先验是否太过于主观？你是否会通过不断调整先验，进而达到任何想要的结果呢？———此时你该如何回应？

贝叶斯的主观性#

在之前我们提到了一个关于贝叶斯统计的常见批评观点——它的主观性。

  • 一些人担心“主观地”调整先验模型会使贝叶斯分析人员得出他们想要的任何结论。

  • 在学习完这节课后我们可以更严谨地回应这个观点。

请根据下面的陈述判断其是真还是假，并提供你的推理：

1、所有的先验选择都是具有信息量的。

2、有可能有充分的理由选择具有信息量的先验。

3、任何先验选择都可以被足够多的数据克服。

4、频率学派的范式是完全客观的。

答案： 1、错误。模糊的先验通常是不具有信息量的。 2、正确。我们可能有充足的先前数据或专业知识来构建我们的先验。 3、错误。如果你将潜在的参数值赋予零先验概率，任何数量的数据都无法改变它！ 4、错误。主观性总是渗透到频率学派和贝叶斯分析中。在贝叶斯范式中，我们至少可以命名和量化这种主观性的方面。

★贝叶斯最大的特点：

  我们不否认主观性的存在，但是我们可以把这种主观性的先验信息公开呈现，每个人都可以来批判，这样我们可以以一种更加公开透明的方式去做推断。

🔍回顾：贝叶斯学派和频率学派的差异对比

任何统计分析方法都不可能完全客观，因此主观性是一个相对概念:

  • 贝叶斯学派的主观性通过先验的设定来体现，透明，不易让人产生误解

  • 频率学派的主观性暗含在各种前提预设中，比如方差分析中的方差齐性和正态性，这种看似‘客观的’预设，一方面难以满足，一方面也是一种主观的设定。

  • 更为宏观的来说，样本的抽取，数据清理方式的选择，分析方法的选择，\(p\)值的设定，这些都存在主观性。因此，频率学派并没有想象的那么‘客观’。

  • 主观不一定是坏事：通过量化方法将个体的经验和专家知识整合到数据分析之中。

频率学派

贝叶斯学派

概率定义：概率是事件在无限重复试验中的频率

概率定义：概率是对假设的信念度量

假设：假设是固定的，数据是随机的

假设：假设是随机的，数据是固定的

推断方式：基于假设检验，通过\(p\)值判断是否拒绝零假设

推断方式：通过更新先验与新数据计算后验概率

置信区间：在重复试验中，95%的区间包含真实参数

可信区间：给出某参数位于区间内的概率（如95%可信度）

\(p\)值：衡量在零假设下，观测数据或更极端数据的概率

后验概率：给出假设为真的更新概率

数据独立性：推断只基于当前试验数据，不考虑先验信息

先验信息：结合历史数据或专家意见，用于更新推断

实验重复性假设：推断基于实验的假想重复性

逐步积累信息：通过结合新数据不断更新和完善假设

适应性：实验设计固定，不能在中途更新或调整

适应性：可以灵活调整试验设计和决策，如自适应试验

来源：

Goligher, E. C., Heath, A., & Harhay, M. O. (2024). Bayesian statistics for clinical research. The Lancet, 404(10457), 1067-1076.

总结：贝叶斯分析确实可以基于“主观”经验建立先验。

  • 在最理想的情况下，这不是件坏事，主观先验可以反映出丰富的过去经验，应该纳入我们的分析中——不这样做是不幸的。即使主观先验与实际观察到的证据相矛盾，随着这些证据的累积，它对后验的影响会逐渐消失。

  • 我们已经见过一个最糟糕的例外情况。而且这是可以预防的。如果主观先验足够顽固和极端，它会将可能的参数值的概率分配为零，那么任何数量的反证据都不足以改变它。

Striking a balance between the prior & data#

  • 我们已经看到不同先验和不同数据对后验分布的影响

  • 实际上，后验分布是两者间的平衡

下面，我们将不同先验和似然结合，观察后验的变化：

# 创建 3x3 的子图布局
fig, axes = plt.subplots(3, 3, figsize=(18, 15))

# 调用绘制函数，对不同的先验和似然进行组合
bayesian_analysis_plot(70, 30, 77, 128, axes[0, 0])
bayesian_analysis_plot(70, 30, 152, 254, axes[0, 1])
bayesian_analysis_plot(70, 30, 231, 385, axes[0, 2])
bayesian_analysis_plot(10, 1, 77, 128, axes[1, 0])
bayesian_analysis_plot(10, 1, 152, 254, axes[1, 1])
bayesian_analysis_plot(10, 1, 231, 385, axes[1, 2])
bayesian_analysis_plot(1, 1, 77, 128, axes[2, 0])
bayesian_analysis_plot(1, 1, 152, 254, axes[2, 1])
bayesian_analysis_plot(1, 1, 231, 385, axes[2, 2])


# 设置 x 轴范围
for ax in axes.flatten():
    ax.set_xlim(0.4, 0.9)

# 调整布局
plt.tight_layout()

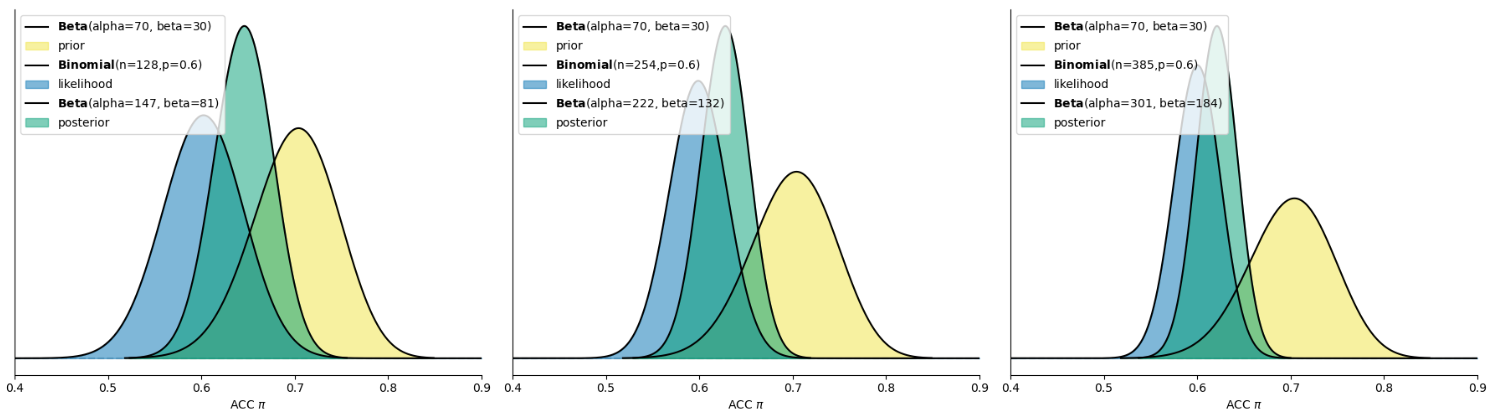
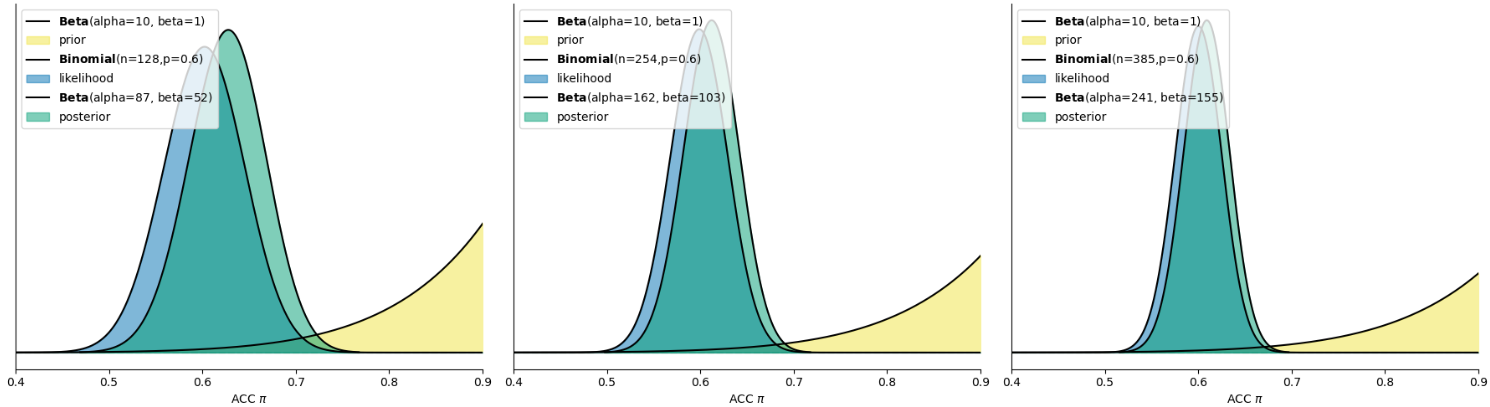
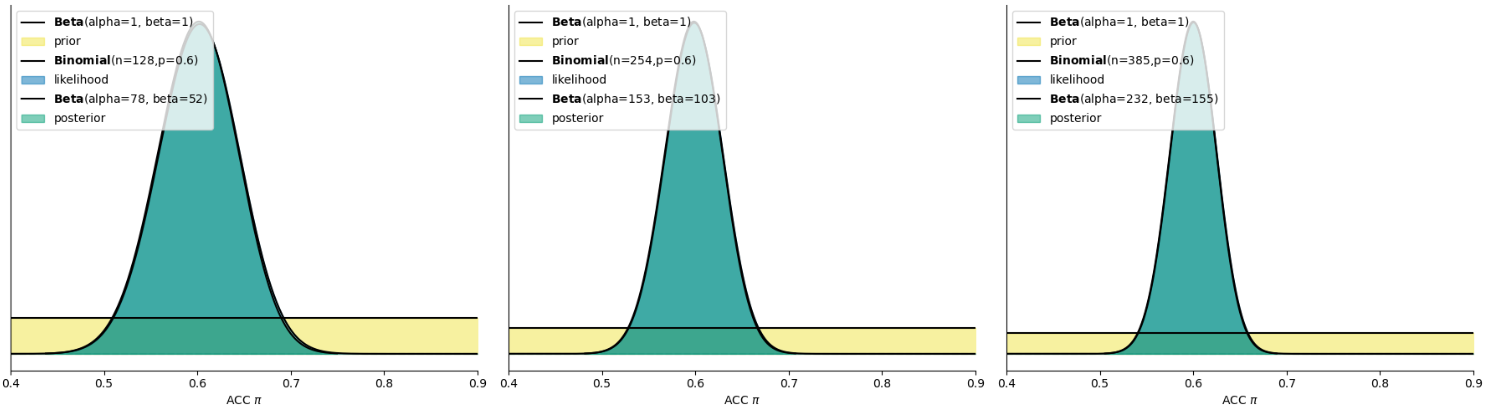
alt text alt text alt text

  • 从左往右： 数据的试次从128增加到385，似然的分布越来越集中，对后验的影响也越来越大。

  • 从上往下： 先验分布从信息型(informative prior)变为模糊型(vague prior)，先验分布对后验分布的影响也就越来越小

  • 最后一列告诉我们，无论不同的人对先验的差异有多大，只要似然的分布够集中，即数据提供的信息足够丰富，那么后验分布主要受到来自数据的影响，不同人的后验分布也并不会相差太大。

💡这里，我们探讨了后验模型在先验模型和数据之间的平衡。总的来说，我们观察到以下趋势：

  • 先验影响：先验越不模糊、越具有信息量，即我们对先验越有确定性，先验对后验的影响就越大。

  • 数据影响：我们拥有的数据越多，数据对后验的影响就越大。因此，即使具有不同的先验，如果两次测量的数据充足并且相似，那么他们的后验结果会非常相似。

  • 此外，我们还看到在序列贝叶斯分析中，随着越来越多的数据的出现，我们逐步更新后验模型。这个后验的最终结果不受观察数据的序列（即后验对数据的顺序不变）或者是一次性观察数据还是逐步观察数据的影响。

代码练习#

练习 4.1：将先验与描述配对

下面列出了五种不同的\(π\)的先验模型。

请用以下描述之一标记每个先验：有些偏向\(π\) < 0.5，有些强烈偏向\(π\) < 0.5，有些将\(π\)置于0.5中心，有些偏向\(π\) > 0.5，有些强烈偏向\(π\) > 0.5。

  • a)Beta(1.8,1.8)

  • b)Beta(3,2)

  • c)Beta(1,10)

  • d)Beta(1,3)

  • e)Beta(17,2)

练习 4.2：将图形与代码配对

下面的绘图函数更可能使用了哪些参数生成了下面的图形？

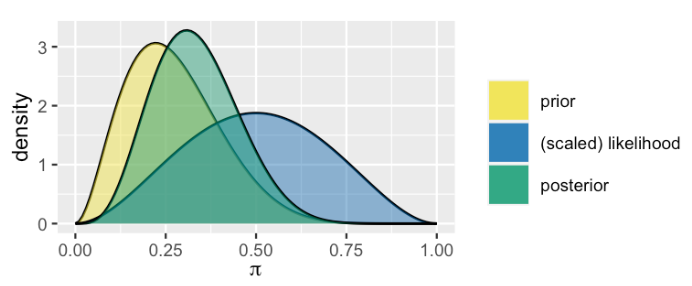
alt text

  • a) alpha = 2, beta = 2, y = 8, n = 11

  • b) alpha = 2, beta = 2, y = 3, n = 11

  • c) alpha = 3, beta = 8, y = 2, n = 6

  • d) alpha = 3, beta = 8, y = 4, n = 6

  • e) alpha = 3, beta = 8, y = 2, n = 4

  • f) alpha = 8, beta = 3, y = 2, n = 4

# 导入数据加载和处理包：pandas
import pandas as pd
# 导入数字和向量处理包：numpy
import numpy as np
# 导入基本绘图工具：matplotlib
import matplotlib.pyplot as plt
# 导入高级绘图工具 seaborn 为 sns
import seaborn as sns
# 导入概率分布计算和可视化包：preliz
import preliz as pz

#---------------------------------------------------------------------------
#                            请替换...填入 Beta 分布参数, alpha 和 beta
#---------------------------------------------------------------------------
# 设置 Beta 分布参数
alpha = ...     # alpha
beta  = ...     # beta

#---------------------------------------------------------------------------
#                            请替换...请填入观测数据 y 和 n
#---------------------------------------------------------------------------
y = ...     # y 代表支持数
n = ...     # n 代表总人数

#---------------------------------------------------------------------------
#                            请使用 bayesian_analysis_plot 进行绘图
#---------------------------------------------------------------------------
bayesian_analysis_plot(...)

答案：

# 答案

#---------------------------------------------------------------------------
#                            请填入 Beta 分布参数，alpha 和 beta
#---------------------------------------------------------------------------
# 设置 Beta 分布参数
alpha = 10     # alpha
beta  = 50     # beta

#---------------------------------------------------------------------------
#                            请填入观测数据 y 和 n
#---------------------------------------------------------------------------
y = 80     # y 代表支持数
n = 180     # n 代表总人数

bayesian_analysis_plot(alpha, beta, y, n)

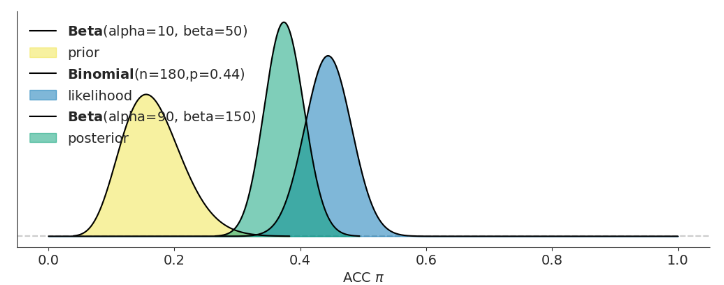
alt text

💐Bonus：使用数学公式证明，后验确实利用了来自先验和似然的信息#

（注：以下涉及的公式包含上一节bonus中的内容）

由于后验分布属于beta分布，因此它的平均值可以写成：

\[ E(\pi |Y=y)=\frac{\alpha + y}{\alpha + \beta + n} \]

我们可以将\(\frac{\alpha + y}{\alpha + \beta + n}\)拆成以下两部分

\[ E(\pi |Y=y)=\frac{\alpha}{\alpha + \beta + n}+\frac{y}{\alpha + \beta + n}=\frac{\alpha}{\alpha + \beta + n}·\frac{\alpha + \beta}{\alpha + \beta}+\frac{y}{\alpha + \beta + n}·\frac{n}{n} \]
\[ =\frac{\alpha + \beta}{\alpha + \beta + n}·\frac{\alpha}{\alpha + \beta}+\frac{n}{\alpha + \beta + n}·\frac{y}{n}=\frac{\alpha + \beta}{\alpha + \beta + n}·E(\pi)+\frac{n}{\alpha + \beta + n}·\frac{y}{n} \]
\[ y:success trial, n:total trials,y/n表示观察到的数据比例 \]

且，

\[ \frac{\alpha + \beta}{\alpha + \beta + n} + \frac{n}{\alpha + \beta + n} = 1 \]

可以看到，后验均值可以被分解为: 权重×先验均值+权重×数据

  • 那么，当数据越多，即n越大时，先验的权重就会更小，接近0，而此时数据的权重也会越大。因此，后验正是权衡了来自先验和似然的信息

Contents