Part 3: 随机变量的贝叶斯模型

Part 3: 随机变量的贝叶斯模型#

1、随机变量#

在之前的分析中，我们讨论的是对某项研究的“可重复性”这样一个单一事件。

同样的逻辑可以应用于更加抽象和一般性的随机变量进行分析。

假设为了研究可重复性问题，一个有能力且资金充足的研究团队计划进行一系列可重复性实验，他们希望知道这些实验成功重复的比例是多少。

首先我们来了解一个概念：胜率或成功率

想象你玩斗地主，有五局三胜，七局四胜这一说，一轮玩下来，就会出现胜率
然而，胜率并不是一成不变的，它会随着每次游戏的输赢而变化
在每一轮开始前，你并不会知道你这次的胜率是多少

在我们的例子中，假设计划对6项研究进行重复实验：

假设该团队对于任何研究成功复现的成功率为\( π，π \)是未知的且可能会变化，所以\( π \)是一个随机变量。
根据团队先前的经验以及心理学研究的现状，我们猜测其成功复现的成功率为\( π \)=50%。
他接下来可能成功复现的次数\(Y\)可能是0，可能是1，也可能是6，可以有7种可能的成功复现次数，\( Y∈ \) {0,1,2,3,4,5,6}。

思考一个问题：虽然我们知道他们的平均成功率为 \( π \)=50%，但问题在于，对于每一种复现成功的次数（1～6），其可能性分别是多少呢？

2、二项式模型#

由于每次重复实验，结果只有两种可能：成功 vs 失败

该团队总共进行6次重复实验，我们想要知道的是成功1次，成功2次，成功3次，…，的概率。

对于这种情况，我们可以用二项分布来分析。

该团队的成功率为\(π\)，在\(π\)下某成功次数发生的概率可表示为：
\( f(y|π)=(^n_y)π^y(1-π)^{n-y} ~~~~~~for~y∈ \) {\( 0,1,2....,n \)} \( (^n_y)=\frac{n!}{y!(n-y)!} \)

\( π \)表示成功的可能性，\( y \)表示在n个试次中成功的次数，二项模型含有的前提假设是：

(1) 所有试次发生都是相互独立的 (2) 在每个试次中，成功的概率都是一个固定的值\(π\)

成功次数为0~6 的可能性可以分别写成：

\( f(Y=0|π=0.5)=(^6_0)0.5^0(1-0.5)^6 \)

\( f(Y=1|π=0.5)=(^6_1)0.5^1(1-0.5)^5 \)

…

\( f(Y=5|π=0.5)=(^6_5)0.5^5(1-0.5)^1 \)

\( f(Y=6|π=0.5)=(^6_6)0.5^6(1-0.5)^0 \)

我们可以使用代码帮助计算，其中P对应公式中的\( π \)。

st.binom.pmf(y, n, p)

In [1]:

# 导入数据加载和处理包：pandas
import pandas as pd
# 导入数字和向量处理包：numpy
import numpy as np
# 导入基本绘图工具：matplotlib
import matplotlib.pyplot as plt
# 导入高级绘图工具 seaborn 为 sns
import seaborn as sns
# 导入统计建模工具包 scipy.stats 为 st
import scipy.stats as st 

# 设置APA 7的画图样式
plt.rcParams.update({
    'figure.figsize': (4, 3),      # 设置画布大小
    'font.size': 12,               # 设置字体大小
    'axes.titlesize': 12,          # 标题字体大小
    'axes.labelsize': 12,          # 轴标签字体大小
    'xtick.labelsize': 12,         # x轴刻度字体大小
    'ytick.labelsize': 12,         # y轴刻度字体大小
    'lines.linewidth': 1,          # 线宽
    'axes.linewidth': 1,           # 轴线宽度
    'axes.edgecolor': 'black',     # 设置轴线颜色为黑色
    'axes.facecolor': 'white',     # 轴背景颜色（白色）
    'xtick.direction': 'in',       # x轴刻度线向内
    'ytick.direction': 'out',      # y轴刻度线向内和向外
    'xtick.major.size': 6,         # x轴主刻度线长度
    'ytick.major.size': 6,         # y轴主刻度线长度
    'xtick.minor.size': 4,         # x轴次刻度线长度（如果启用次刻度线）
    'ytick.minor.size': 4,         # y轴次刻度线长度（如果启用次刻度线）
    'xtick.major.width': 1,        # x轴主刻度线宽度
    'ytick.major.width': 1,        # y轴主刻度线宽度
    'xtick.minor.width': 0.5,      # x轴次刻度线宽度（如果启用次刻度线）
    'ytick.minor.width': 0.5,      # y轴次刻度线宽度（如果启用次刻度线）
    'ytick.labelleft': True,       # y轴标签左侧显示
    'ytick.labelright': False      # 禁用y轴标签右侧显示
})

In[2]:

y = [0,1,2,3,4,5,6]  # 成功次数 
n = 6                # 重复研究总次数
p = 0.5              # 假设的成功概率

# 计算概率值
prob = st.binom.pmf(y, n, p)

result_table = pd.DataFrame({"成功次数":y, "概率":prob})
result_table

显然，当团队的成功概率为 0.5 时，其在六次研究中获得 y = 3 次成功的概率最高(p = 0.3125)。

In [3]:

# 绘制灰色竖线
for i, j in zip(y , prob):
    plt.plot([i, i], [j, 0], 'gray', linestyle='-', linewidth=1, zorder=1, )

# 绘制黑色点(各成功率次数的成功率)
plt.scatter(y, prob, c='black')

plt.ylabel('$f(y|\pi)$')
plt.xlabel('y')

plt.xlim(-0.2,6.2)
plt.ylim(0,0.5)
plt.show()

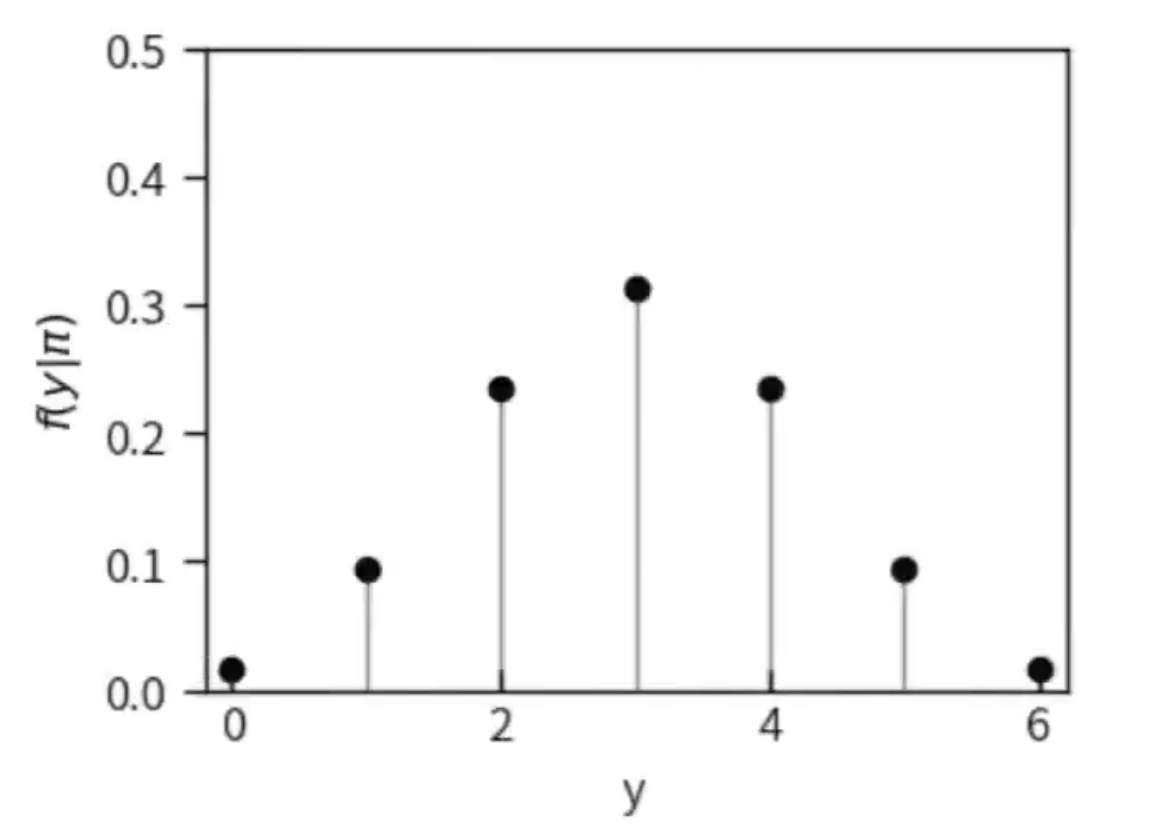
3、概率质量密度函数（probability mass function, pmf）#

概率质量密度函数：是用来描述离散型随机变量在各特定取值上的概率。

从上图我们可以看出，成功次数y在不同的取值上的概率不同。

由于y的个数是有限的，并且是随机发生的，我们把y称为离散型随机变量，而y发生的概率\( f(y) \)则被称为概率质量函数。

对于离散型随机变量\( Y \)，\( Y \)各取值的概率由\( f(y) \)指定：

\( f(y)=P(Y = y) \)

并且有如下性质：

对所有y的取值来说，\( 0 ≤ f(y) ≤ 1 \)
\( ∑_{ally} f(y)=1 \)，y取值的所有概率之和为1

In [4]:

sum(result_table['概率'])

4、二项似然函数(The Binomial likelihood function)#

不同的信念

虽然我们认为该团队重复6个实验的成功率是50%，但并非所有人都这么认为。

乐观派认为该团队的成功概率为 0.8，表示对实验成功复现持高度信心。
悲观派则认为该团队的成功概率仅为 0.2，意味着对实验成功复现不太乐观。

成功的概率影响着他们对研究复现结果的预期：

如果团队的成功概率高，那么6次研究中成功复现的次数会更多。
反之，如果成功概率低，那么研究复现的失败次数就会更多。

我们可以计算持不同信念的人心中，该团队在6项研究中成功复现的次数的概率分布并画图。

In [5]:

y = [0,1,2,3,4,5,6]  # 成功次数 
n = 6                # 研究总次数

# 计算似然值
p = 0.5              # 根据以往战绩假设的成功概率
likelihood1 = st.binom.pmf(y, n, p)
p = 0.8              # Kasparov支持者眼中的成功概率
likelihood2 = st.binom.pmf(y, n, p)
p = 0.2              # 深蓝支持者眼中的成功概率
likelihood3 = st.binom.pmf(y, n, p)

result_table = pd.DataFrame({
  "成功次数":y, 
  "本团队(pi=0.5)":likelihood1, 
  "悲观派(pi=0.2)":likelihood2, 
  "乐观派(pi=0.8)":likelihood3})
result_table

In [6]:

# 创建子图
fig, axs = plt.subplots(1, 3, figsize=(10, 4))

# 绘制三个图,每个子图类似原图
three_pi = ["Team itself ($\pi = 0.5$)","Optimists ($\pi = 0.8$)","Pessimists ($\pi = 0.2$)"]
likelihoods = [likelihood1, likelihood2, likelihood3]
for i, ax in enumerate(axs):
    
    ax.scatter(y, likelihoods[i], c='black')
    
    for xx, yy in zip(y, likelihoods[i]):
        ax.plot([xx, xx], [yy, 0], 'gray', linestyle='-', linewidth=1, zorder=1)
    
    # 添加facet
    ax.set_title(three_pi[i])

    ax.set_xlim(-0.2,6.2)
    ax.set_ylim(0,0.4)

fig.supylabel('$f(y|\pi)$')
fig.supxlabel('y')
plt.tight_layout()
plt.show()

显然，对于乐观派来说，团队取得六次成功的概率远高于其他成功次数。而对于悲观派来说，团队全败的可能性远高于其他成功次数。

换句话说，若团队在6项研究中仅成功复现一次，这种情况在低成功率下(悲观派设想的情境)更可能出现，在高成功率下(乐观派设想的情境)几乎不可能出现。
那么团队成功重复的成功率，更可能(likelihood)是悲观派设想的那样(\( π=0.2 \))。

例如，在乐观派和悲观派眼中(不同成功率\( π \)下)，6项研究只成功1次的可能性(即似然，likelihood)。

In [7]:

# 定义成功次数和研究总次数
y = 1  # 成功次数，作为数组处理以便向量化计算
n = 6  # 研究总次数

# 计算似然值，对于三种不同的成功概率 p
p_values = [0.5, 0.8, 0.2]          # 定义三种成功率
likelihoods = []                    # 用于存储每种成功率的似然值结果

for p in p_values:
    likelihood = st.binom.pmf(y, n, p)  # 使用st.binom.pmf计算似然值
    likelihoods.append(likelihood)      # 将结果添加到列表中


# 创建图形和子图
fig, ax = plt.subplots()  # 此处应该是 plt.subplots() 而不是 plt.subplot()
ax.scatter(p_values, likelihoods, c='black')
# 设置x轴和y轴的限制应该在绘制线条之前完成，以避免重复设置
ax.set_xlim(-0.2, 1.2)  # x轴范围根据p_values调整，最大不应超过1
ax.set_ylim(0, 0.5)
for xx, yy in zip(p_values, likelihoods):
    ax.plot([xx, xx], [0, yy], 'gray', linestyle='-', linewidth=1, zorder=1)
    # 注意这里的顺序是 [0, yy] 而不是 [yy, 0]，因为我们希望从x轴画到对应的似然值
# 设置坐标轴标签，直接使用ax的方法，而不是fig的方法
ax.set_ylabel('$f(\pi|y)$')  # 使用ax.set_ylabel而不是fig.supylabel
ax.set_xlabel('$\pi$')         # 使用ax.set_xlabel而不是fig.supxlabel
plt.tight_layout()  # 调整布局以避免标签重叠
plt.show()

5、似然函数#

当团队只成功复现一次时，该事件在不同成功率下出现的可能性可以写为：

\( f(Y=1|π=0.2)=(^6_1)0.2^1(1-0.2)^5 \)

\( f(Y=1|π=0.5)=(^6_1)0.5^1(1-0.5)^5 \)

\( f(Y=1|π=0.8)=(^6_1)0.8^1(1-0.8)^5 \)

因此，成功复现次数为1时的似然函数可以写成：

\( L(π|y=1)=f(y=1|π)=(^6_1)π^1(1-π)^{6-1}=6π(1-π)^5 \)

不同成功率下的似然：

\( π \)	0.2	0.5	0.8
\( f(π \vert y=1) \)	0.3932	0.0938	0.0015

注意：

似然函数表示的是，在各种可能的成功率π下,成功次数Y=1的可能性，所以

该似然函数公式只取决于π
似然函数的总和加起来不为1（从条件概率的公式来看，似然函数的分母是不同的）

条件概率 vs 似然函数

当\( π \)是一定时，条件概率质量函数\( f(·|π) \)可以帮我们计算在π取值下（各种模型），不同的数据\( Y(e.g., y1,y2) \)发生的可能性。

\( f(y_1|π)~vs~f(y_2|π) \)

当\( Y=y \)一定时，似然函数\( L(·|y)=f(y|·) \)允许我们比较在各种不同的模型，即二项式的\( π \)取值\( （e.g., π_1,π_2） \)下，观察到这个数据y的可能性（relative likelihood）

\( L(π_1|y)与L(π_2|y) \)

即

\( f(y|π_1)与f(y|π_2) \)

在二项分布模型下：

进行n=6个重复实验时，成功次数与成功率的关系符合二项式模型，可以用如下的形式来表示：

\( Y|π\sim Bin(6,π) \)

\( f(y|π)=(^6_y)π^y(1-π)^{6-y}~~~~~~~for~y\in \) {0,1,2,3,4,5,6}

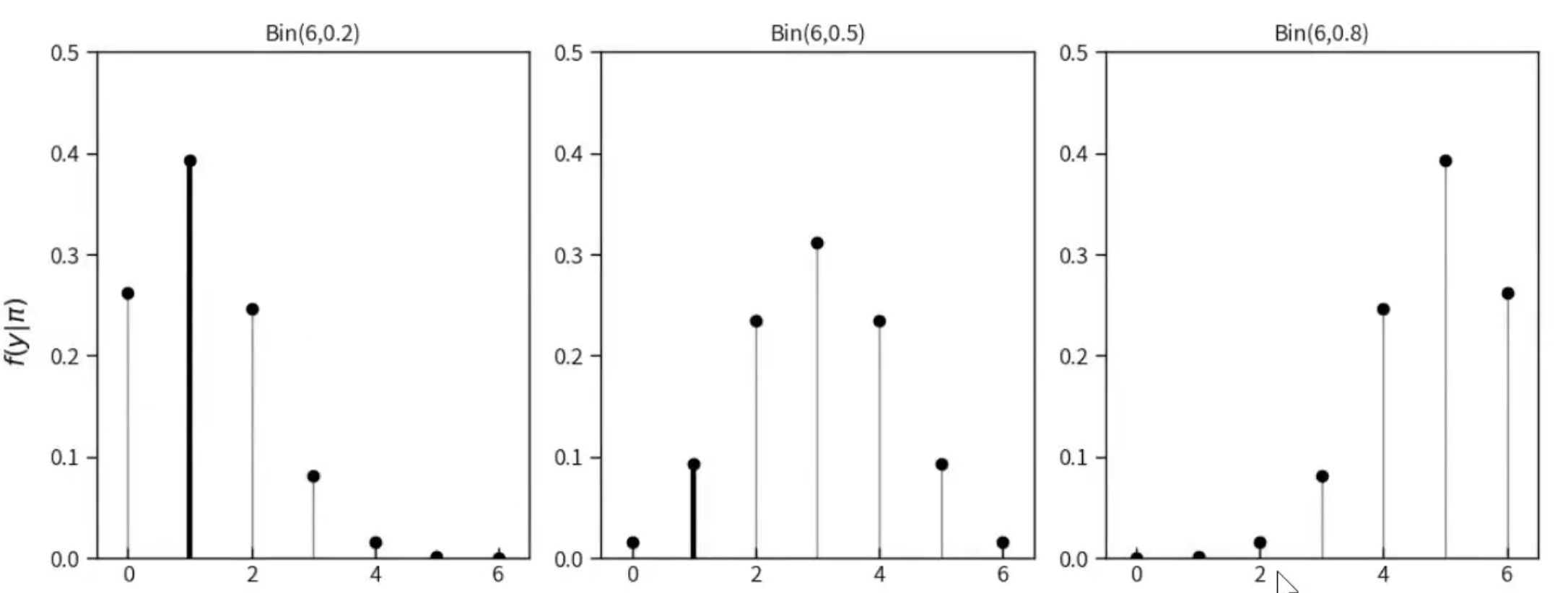
下图给出了几种\( π \)的取值，我们可以通过概率模型得到每种\( Y \)发生的可能性。

同时，我们可以看到，\( Y=1 \)(赢一次)这一特定的数据模式，在各个\( π \) 取值(模型)下的似然。

In [8]:

# Values for Y (number of successes in n trials)
y = np.arange(0, 7)
# Number of trials (n) and different probabilities (π values)
n = 6
pi_values = [0.2, 0.5, 0.8]

# Create subplots
fig, axs = plt.subplots(1, 3, figsize=(12, 5))
# Loop over each pi value to plot the corresponding binomial distribution
for i, pi in enumerate(pi_values):
    # Calculate binomial probabilities for each y (number of successes)
    likelihoods = st.binom.pmf(y, n, pi)
    
    # Scatter plot of the likelihoods
    axs[i].scatter(y, likelihoods, color='black', zorder=2)
    
    # Draw gray vertical lines
    for yy, likelihood in zip(y, likelihoods):
        axs[i].plot([yy, yy], [0, likelihood], color='gray', linestyle='-', linewidth=1, zorder=1)
    
    # Highlight y = 1 with a black line
    axs[i].plot([1, 1], [0, st.binom.pmf(1, n, pi)], color='black', linewidth=3, zorder=3)
    
    # Title with binomial parameters
    axs[i].set_title(f'Bin({n},{pi})')
    
    # Set y and x axis limits
    axs[i].set_xlim(-0.5, 6.5)
    axs[i].set_ylim(0, 0.5)

# Global labels
fig.supylabel(r'$f(y|\pi)$')
fig.supxlabel('y')

# Adjust layout for better fit
plt.tight_layout()
plt.show()

6、先验概率模型(Prior probability model)#

建立先验模型

从前面的描述可以看到，二项分布的参数π也可以变化，也可以成为一个随机变量。

例如，我们想当一个更有深度的观察者，融合了乐观派、悲观派和中立者三者关于π的估计。
但是，我们对三种观点的可能性有不同的信念。

假如我们总体上是一个乐观派，但不排除悲观派的观点，我们给三派观点分配了一定的概率(先验)。

例如，设定\( π_{0.2}=0.1 \)，或者\( π_{0.2}=0.5 \)。但需要所有\( f(π) \)的总和为1。

\( π \)	0.2	0.5	0.8	total
\( f(π) \)	0.10	0.25	0.65	1

我们设定的π的数量也是可以变化的。

例如，我们还可以将一种非常悲观的可能性也纳入进来，认为该团队成功率为0.01，即\( π \)=0.01。
那么新形成的先验分布可能如下。

\( π \)	0.01	0.2	0.5	0.8	total
\( f(π) \)	0.10	0.10	0.25	0.55	1

7、后验概率模型(Posterior probability model)#

前述第一个先验模型，我们总体上是乐观的，认为团队高成功率的可能性很高 (\( π_{0.8}=0.65 \))。

\( π \)	0.2	0.5	0.8	total
\( f(π) \)	0.10	0.25	0.65	1

然而，最终结果发现：该团队只成功复现一次。

这个新的数据会如何改变我们的信念？

我们可以综合先验和似然，根据贝叶斯的思路，计算后验概率。

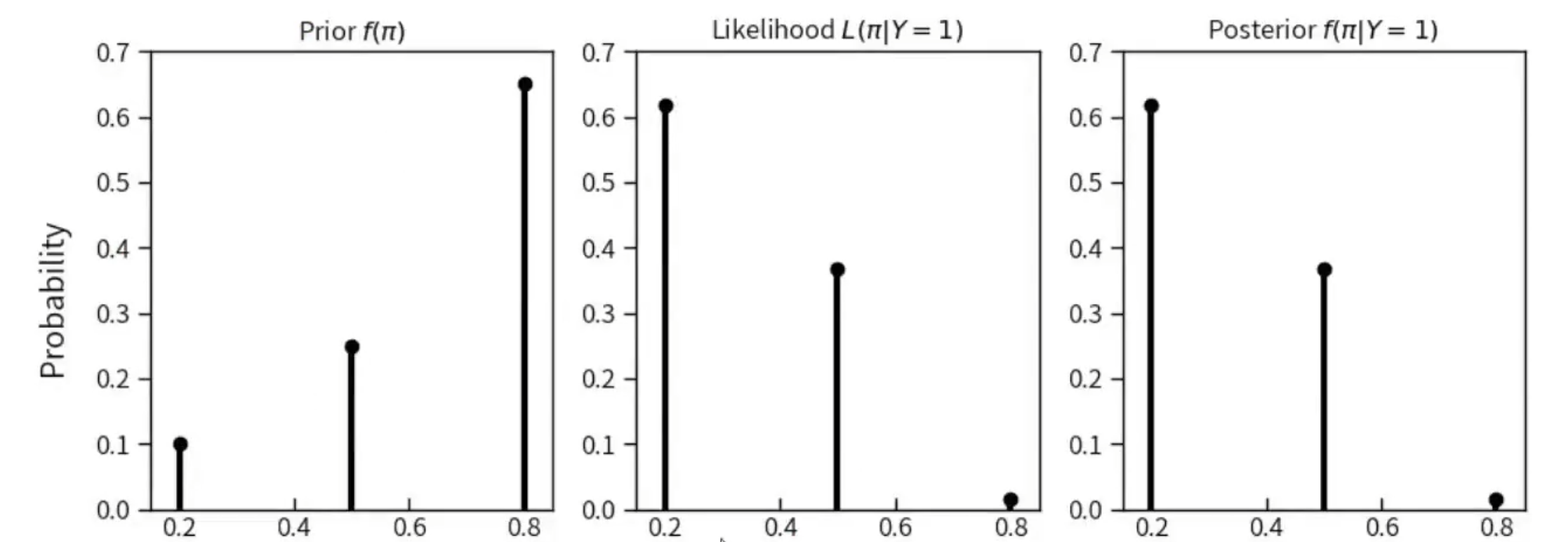
其中团队成功复现的概率从\( π_{0.8}=0.65 \)降低为\( π_{0.8}=0.015 \)。意味着，他成功率为0.2的可能性是最大的\( π_{0.2}=0.617 \)。

左图为先验模型
中间的图为似然模型
右边的图为后验模型

In [9]:

# Pi values and corresponding data
pi_values = [0.2, 0.5, 0.8]
f_pi = [0.10, 0.25, 0.65]  # Prior probabilities
L_pi_given_Y1 = [0.617, 0.367, 0.015]  # Likelihoods given Y=1
posterior = [0.617, 0.367, 0.015]  # Posterior, assumed same as likelihoods here

# Create subplots for prior, likelihood, and posterior
fig, axs = plt.subplots(1, 3, figsize=(10, 4))

# Prior Probability f(π)
axs[0].scatter(pi_values, f_pi, color='black', zorder=2)
for xx, yy in zip(pi_values, f_pi):
    axs[0].plot([xx, xx], [0, yy], color='black', linewidth=3, zorder=1)
axs[0].set_title(r'Prior $f(\pi)$')
axs[0].set_xlim(0.15, 0.85)
axs[0].set_ylim(0, 0.7)

# Likelihood L(π|Y=1)
axs[1].scatter(pi_values, L_pi_given_Y1, color='black', zorder=2)
for xx, yy in zip(pi_values, L_pi_given_Y1):
    axs[1].plot([xx, xx], [0, yy], color='black', linewidth=3, zorder=1)
axs[1].set_title(r'Likelihood $L(\pi|Y=1)$')
axs[1].set_xlim(0.15, 0.85)
axs[1].set_ylim(0, 0.7)

# Posterior Probability f(π|Y=1)
axs[2].scatter(pi_values, posterior, color='black', zorder=2)
for xx, yy in zip(pi_values, posterior):
    axs[2].plot([xx, xx], [0, yy], color='black', linewidth=3, zorder=1)
axs[2].set_title(r'Posterior $f(\pi|Y=1)$')
axs[2].set_xlim(0.15, 0.85)
axs[2].set_ylim(0, 0.7)

# Set labels and layout
for ax in axs:
    ax.set_xlabel(r'$\pi$')

fig.supylabel('Probability')
plt.tight_layout()
plt.show()

后验模型的计算过程

上图所表示的后验可写成：

\( f(π|y)=1 \)

表示当团队只成功复现一项研究时，他成功率\(π\)的概率分布

根据贝叶斯公式，我们可以进一步对后验概率公式进行展开：

\( posterior=\frac{prior*likelihood}{normalizing~constant} \)

\( f(π|y=1)=\frac{f(π)L(π|y=1)}{f(y=1)}~~~~~for~π\in 0.2,0.5,0.8 \)

\( f(π=0.2|y=1)=\frac{0.10×0.3932}{0.0637}≈0.617 \)

\( f(π=0.5|y=1)=\frac{0.25×0.0938}{0.0637}≈0.368 \)

\( f(π=0.8|y=1)=\frac{0.65×0.0015}{0.0637}≈0.015 \)

下表对后验概率模型进行了总结，我们可知，经过了先前只成功了一项研究的复现经历后，该团队取得成功(\( π=0.8 \))的可能性已经从0.65降到了0.015

\( π \)	0.2	0.5	0.8	total
\( f(π) \)	0.10	0.25	0.65	1
\( f(π \vert y=1 \))	0.617	0.368	0.015	1

补充材料

省略分母的计算

考虑到分母是一个常数，我们常常会成功率计算它

省略分母后验的计算可写成：

\( f(π=0.2|y=1)=c·0.10·0.3932∝0.039320 \) \( f(π=0.5|y=1)=c·0.25·0.0938∝0.023450 \) \( f(π=0.8|y=1)=c·0.65·0.0015∝0.000975 \)

∝表示成比例，尽管这些未经标准化的后验概率总和不等于1

0.039320+0.023450+0.000975=0.063745

但它们的比例关系并未改变（见下图）

In [10]:

# Pi values and corresponding unnormalized posterior data
pi_values = [0.2, 0.5, 0.8]
unnormalized_posterior = [0.03932, 0.02345, 0.000975]  # Unnormalized posterior values
normalized_posterior = [val / sum(unnormalized_posterior) for val in unnormalized_posterior]  # Normalized

# Create subplots for normalized and unnormalized posteriors
fig, axs = plt.subplots(1, 2, figsize=(8, 4))

# Normalized posterior
axs[0].scatter(pi_values, normalized_posterior, color='black', zorder=2)
for xx, yy in zip(pi_values, normalized_posterior):
    axs[0].plot([xx, xx], [0, yy], color='black', linewidth=3, zorder=1)
axs[0].set_title('Normalized $f(\pi | y=1)$')
axs[0].set_xlim(0.15, 0.85)
axs[0].set_ylim(0, 0.7)

# Unnormalized posterior
axs[1].scatter(pi_values, unnormalized_posterior, color='black', zorder=2)
for xx, yy in zip(pi_values, unnormalized_posterior):
    axs[1].plot([xx, xx], [0, yy], color='black', linewidth=3, zorder=1)
axs[1].set_title('Unnormalized $f(\pi | y=1)$')
axs[1].set_xlim(0.15, 0.85)
axs[1].set_ylim(0, 0.05)

# Set labels and layout
for ax in axs:
    ax.set_xlabel(r'$\pi$')

fig.supylabel('Probability')
plt.tight_layout()
plt.show()

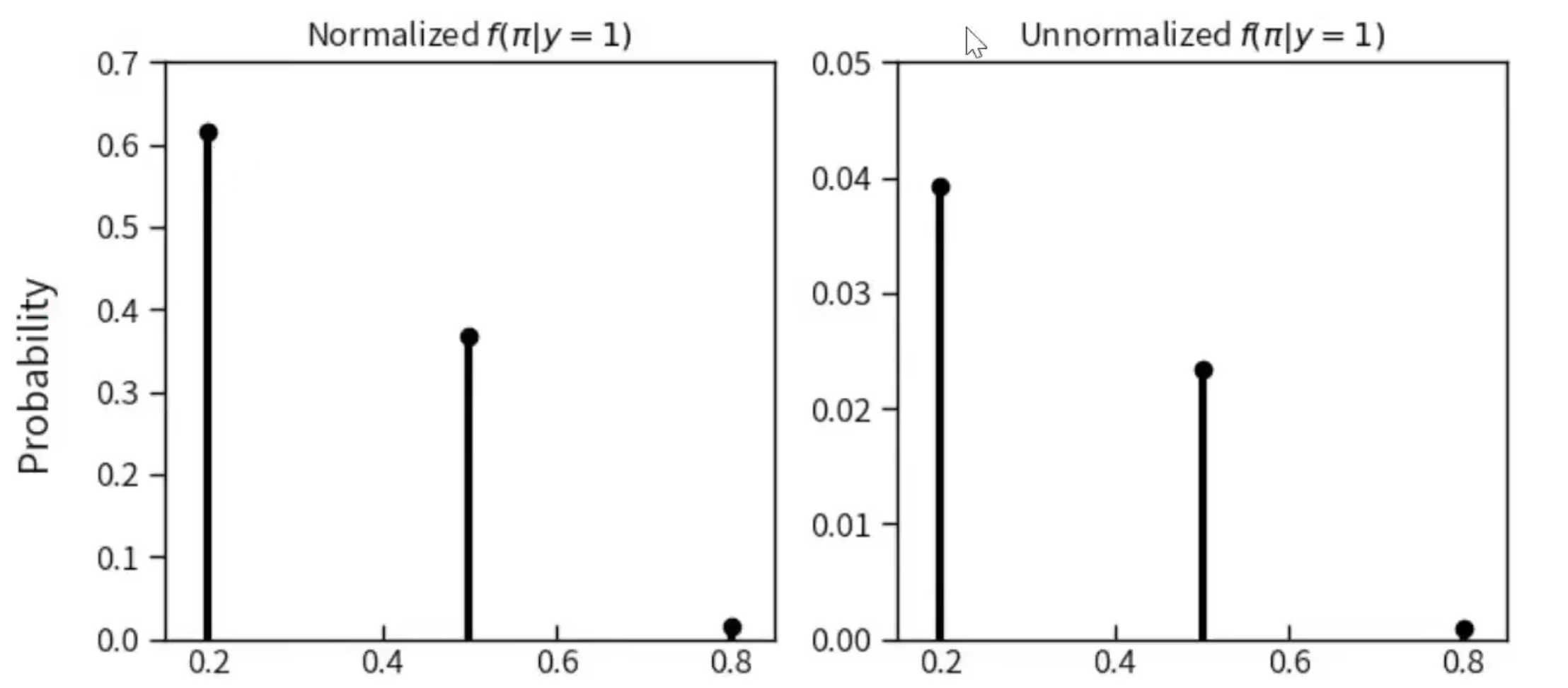
我们可以使用这些未经标准化的后验概率总和作为分母，来对后验概率进行标准化，会得到相同的计算结果。

\( f(π=0.2|y=1)=\frac{0.039320}{0.039320+0.023450+0.000975} \)

注意，分母为所有似然值的总和，因此后验概率的计算公式还可以写成：

\( f(π|y)=\frac{f(π)L(π|y)}{f(y)}=\frac{f(π)L(π|y)}{\sum _{allπ}f(π)L(π|y)} \)

Proportionality

既然\( f(y) \)是一个用来标准化的常数，它并不受\( π \)的影响，那么后验概率质量函数\( f(π|y) \)就与\( f(π) \)和\( L(π|y) \)成正比

\( f(π|y)=\frac{f(π)L(π|y)}{f(y)}∝f(π)L(π|y) \)

\( posterior∝prior·likelihood \)

😜这个性质很重要。因为分母的计算量往往比较大，需要遍历所有参数，如果参数不止一个，计算量可想而知。因此，如过能不计算分母也能计算后验，那么这样的方法(后面会介绍的MCMC算法)将会非常有实践意义。

8、Posterior simulation (with code)#

定义先验模型

定义多个可能的成功率
定义每个成功率出现的可能性 (注意，其和为1)

In [11]:

import pandas as pd
import numpy as np

# 定义可能的成功率
replicated = pd.DataFrame({'pi':[0.2, 0.5, 0.8]})

# 定义先验模型
prior = [0.10, 0.25, 0.65]

模拟在特定成功率下，6项研究中的成功次数

重复这个过程10000次

In [12]:

# 设置随机数种子保证可重复性
np.random.seed(84735)

# 从先验中抽取10000个 pi 值，并生成对应的y值

replicated_sim = replicated.sample(n=10000, weights=prior, replace=True)
replicated_sim['y'] = np.random.binomial(n=6, p=replicated_sim['pi'], size=len(replicated_sim))
replicated_sim.head(10)

In [13]:

#对pi的抽取情况进行总结
replicated_counts =  replicated_sim['pi'].value_counts().reset_index()

replicated_counts.columns = ['pi','n']

replicated_counts['percentage'] = (replicated_counts['n']/len(replicated_sim))

replicated_counts = replicated_counts.sort_values(by='pi')

print(replicated_counts)

不同成功率下，不同成功次数的分布情况f(y|π)

In [14]:

# 导入绘图工具 seaborn
import seaborn as sns
# 通过 facegrid 方法根据不同变量绘制不同的图形
replicated_lik = sns.FacetGrid(replicated_sim,col="pi")
replicated_lik.map(sns.histplot,'y',stat='probability',discrete=True)
plt.tight_layout()
plt.show()

查看\(y=1\)时，对应的\(π\)的分布情况

In [15]:

replicated_post = replicated_sim[replicated_sim['y'] == 1].value_counts()
replicated_post

replicated_post = replicated_sim[replicated_sim['y'] == 1]

replicated_post_plot = sns.histplot(data = replicated_post, x="pi")

#plt.xticks(np.arange(0.2,0.8,0.3))

replicated_post_plot.set(xticks=[0.2,0.5,0.8])
sns.despine()

思考：频率学派(经典统计)会如何处理上述两个问题？

某项研究的可重复性
重复6次的成功率