Model2: Hierarchical model with varying slopes(变化斜率模型)

• 上一个模型考虑了回归截距随站点的变化，在模型2中，我们假设不同站点间的回归截距保持不变，但回归斜率随站点变化。

\[ \beta_{1j}|\beta_1,\sigma_1 \sim N(\beta_1,\sigma_1^2) \]

类似于模型1，模型2的定义形式为：

prior

\[\begin{split} \beta_0 \sim N(0,50^2)\\ \beta_1 \sim N(0,5^2)\\ \sigma_y \sim Exp(1)\\ \sigma_1 \sim Exp(1) \end{split}\]

likelihood

\[ \beta_{1j}|\beta_1,\sigma_1 \overset{ind}{\sim}N(\beta_1,\sigma_1^2)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~Layer2:全局水平（表示斜率在站点间的变化） \]

\[ Y_{ij}|\beta_{0},\beta_{1j},\sigma_y \sim N(\mu_{ij},\sigma_y^2)~with~~\mu_{ij}=\beta_0+\beta_{1j}X_{ij}~~~Layer1:被试水平（表示每个站点内的线性模型） \]

# 定义函数来构建和采样模型
def run_var_slope_model():

    #定义数据坐标，包括站点和观测索引
    coords = {"site": df_first5["Site"].unique(),
            "obs_id": df_first5.obs_id}

    with pm.Model(coords=coords) as model:
        #定义全局参数
        beta_0 = pm.Normal("beta_0", mu=0, sigma=50)
        beta_1 = pm.Normal("beta_1", mu=0, sigma=5) 
        beta_1_sigma = pm.Exponential("beta_1_sigma", 1)
        sigma_y = pm.Exponential("sigma_y", 1) 

        #传入自变量、获得观测值对应的站点映射
        x = pm.MutableData("x", df_first5.stress, dims="obs_id")
        site = pm.MutableData("site", df_first5.site_idx, dims="obs_id") 

        #模型定义
        beta_1j = pm.Normal("beta_1j", mu=beta_1, sigma=beta_1_sigma, dims="site")

        #线性关系
        mu = pm.Deterministic("mu", beta_0+beta_1j[site]*x, dims="obs_id")

        # 定义 likelihood
        likelihood = pm.Normal("y_est", mu=mu, sigma=sigma_y, observed=df_first5.scontrol, dims="obs_id")

        var_slope_trace = pm.sample(draws=5000,           # 使用mcmc方法进行采样，draws为采样次数
                            tune=1000,                    # tune为调整采样策略的次数，可以决定这些结果是否要被保留
                            chains=4,                     # 链数
                            discard_tuned_samples= True,  # tune的结果将在采样结束后被丢弃
                            random_seed=84735,
                            target_accept=0.99)
    
    return model, var_slope_trace

# 注意，以下代码可能运行5分钟左右

var_slope_model, var_slope_trace = run_var_slope_model()

pm.model_to_graphviz(var_slope_model)

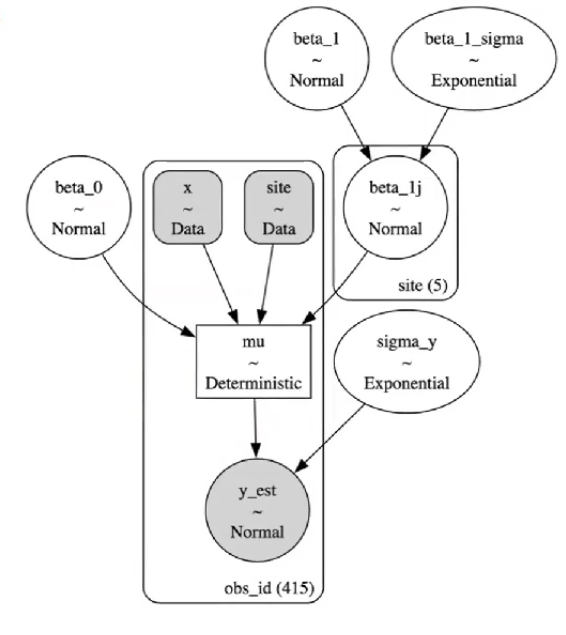
MCMC采样&后验参数估计

var_slope_para = az.summary(var_slope_trace,
                            var_names=["beta_0","beta_1j"],
                            filter_vars="like")
var_slope_para

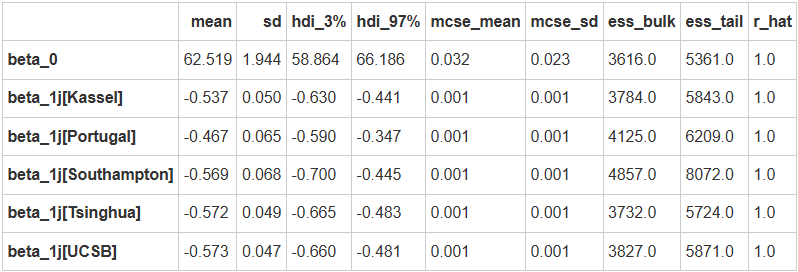
• 可以看出5条回归线的截距一致，但斜率不同

az.plot_forest(var_slope_trace,
           var_names=["~mu", "~sigma", "~offset", "~beta_0"],
           filter_vars="like",
           combined = True)

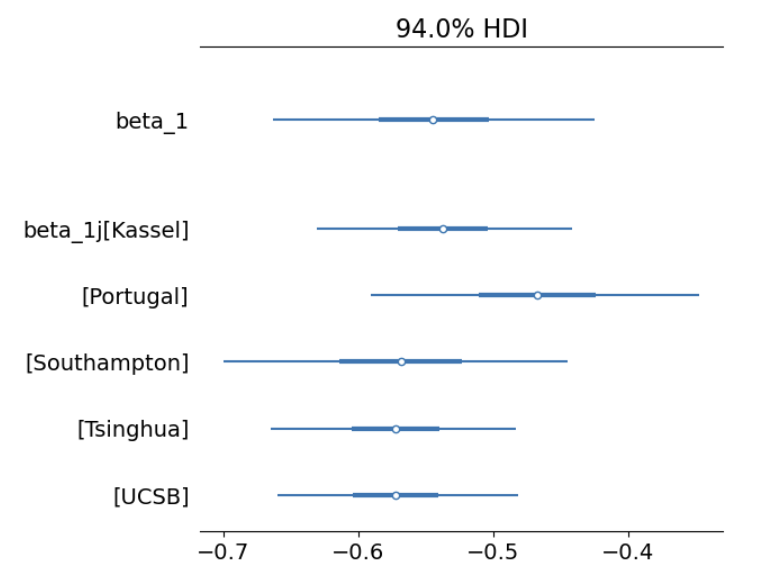
后验预测回归线

#定义函数，绘制不同站点下的后验预测回归线
def plot_partial_regression(data, trace, group_index):
    # 定义画布，根据站点数量定义画布的列数
    fig, ax = plt.subplots(1,len(data["Site"].unique()), 
                       sharex=True,
                       sharey=True,
                       figsize=(15,5))
    
    # 根据站点数来分别绘图
    # 需要的数据有原始数据，每一个因变量的后验预测均值
    # 这些数据都储存在后验参数采样结果中，也就是这里所用的trace
    for i, group in enumerate(data["Site"].unique()):
        #绘制真实数据的散点图
        x = trace.constant_data.x.sel(obs_id = group_index[f"{group}"])
        y = trace.observed_data.y_est.sel(obs_id = group_index[f"{group}"])
        mu = trace.posterior.mu.sel(obs_id = group_index[f"{group}"])
        ax[i].scatter(x, y,
                color=f"C{i}",
                alpha=0.5)
        #绘制回归线
        ax[i].plot(x, mu.stack(sample=("chain","draw")).mean(dim="sample"),
                color=f"C{i}",
                alpha=0.5)
        ax[i].set_title(f"Slope: {var_slope_para.loc[f'beta_1j[{group}]']['mean']}", fontsize=12)
        #绘制预测值95%HDI
        az.plot_hdi(
            x, mu,
            hdi_prob=0.95,
            fill_kwargs={"alpha": 0.25, "linewidth": 0},
            color=f"C{i}",
            ax=ax[i])
        
    # 生成横坐标名称
    fig.text(0.5, 0, 'Stress', ha='center', va='center', fontsize=12)
    # 生成纵坐标名称
    fig.text(0.08, 0.5, 'Self control', ha='center', va='center', rotation='vertical', fontsize=12)
    # 生成标题
    plt.suptitle("Posterior regression models(varing slope)", fontsize=15, y=1.05)
        
    sns.despine()

plot_partial_regression(data=df_first5,
                trace=var_slope_trace,
                group_index=first5_index)

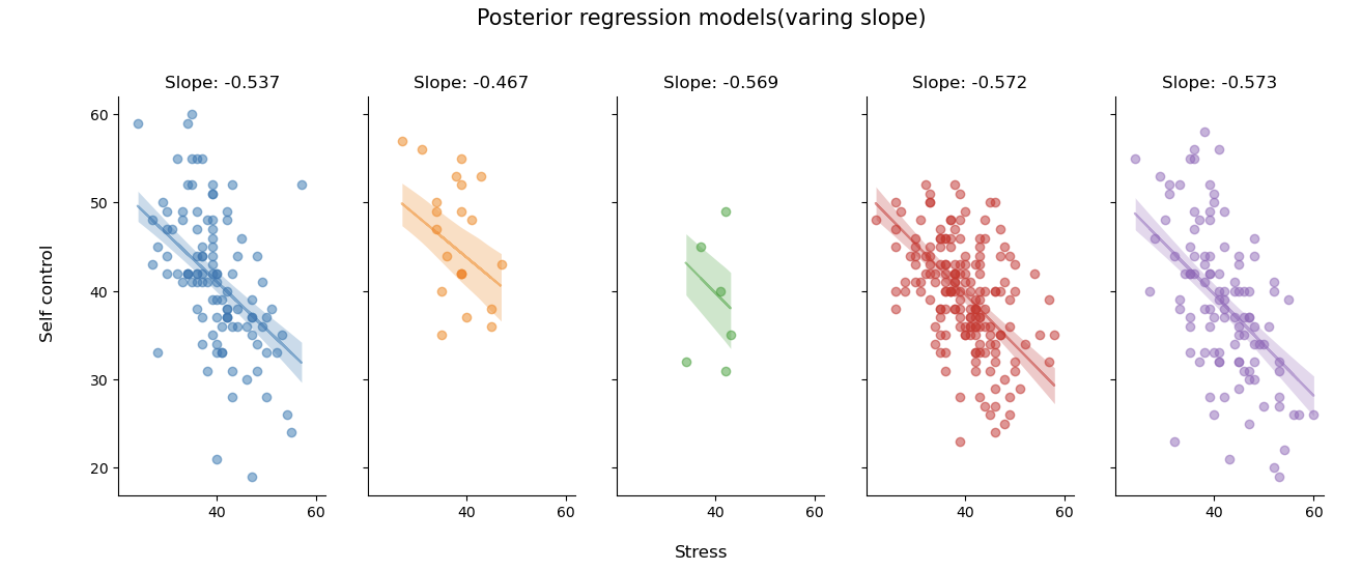
• 不同站点回归线的斜率有所变化，并且不确定性也有所不同。

组间方差与组内方差

在这个模型定义中，组间方差来自beta_1_offset，组内方差来自sigma_y。

# 提取组间和组内变异
calculate_var_odds(var_slope_trace)

被组间方差所解释的部分： 0.03875932652835885 被组内方差所解释的部分： 0.9612406734716412 组内相关： 0.03875932652835885