似然对后验的影响#
从以上分布图可以看出,三种似然分布的均值虽然都是0.60,但随着样本量的增大,似然的分布变得越窄,分布向0.6集中,说明其似然反映的信息也越加集中。
注意:在似然中,y轴为\(f(y|\pi)\),表示在特定的\(\pi\)值下产生当前数据的相对可能性。
那么,不同数据条件下的似然对后验分布的影响是怎么样的呢?
同样的,我们通过可视化分布直观的观察不同数据条件下的后验分布:
(1) 使用公式快速计算出三种数据条件下的后验beta分布中的参数:
Situations |
Data (y, n) |
Posterior |
|---|---|---|
a |
y = 77, n = 128 |
Beta(70 + 77, 30 + 128 - 77) = Beta(147, 81) |
a+b |
y = 152, n = 254 |
Beta(70 + 152, 30 + 254 - 152) = Beta(222, 132) |
a+b+c |
y = 231, n = 385 |
Beta(70 + 231, 30 + 385 - 231) = Beta(301, 184) |
(2) 使用python进行绘制先验分布以及三种数据条件下的似然分布与后验beta分布:
# 定义先验分布的 alpha 和 beta
alpha = 70
beta = 30
# 根据数据定义不同的二项分布数据 (y, n)
data_list = [(77, 128), (152, 254), (231, 385)]
# 创建一个包含三个子图的画布
fig, axes = plt.subplots(1, 3, figsize=(15, 5), sharex=True, sharey=True)
for i, ax in enumerate(axes):
bayesian_analysis_plot(alpha=alpha, beta=beta, y=data_list[i][0], n=data_list[i][1], ax=ax, plot_posterior=True)
ax.set_xlim(0.4,0.9)
# 显示图形
plt.tight_layout()
plt.show()
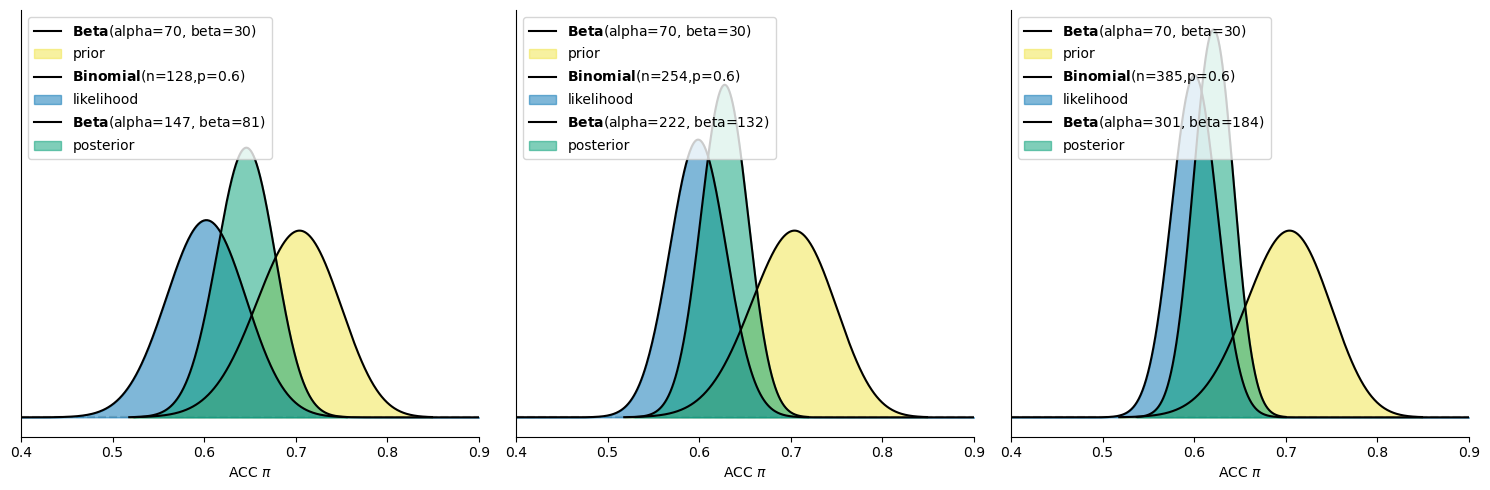
依据以上绘制出的分布图可以得出:
1个 block的情况:进行了 128 次试次,其中有 77 次(60%)判断为正确
样本量较小,似然分布较宽,意味着观测数据对正确率\(\pi\)的约束不强,反映出不确定性较高。此时后验分布处在似然与先验的中间。
2个 block的情况:一共进行了 254 次试次,其中有 152 次(60%)判断为正确
随着样本量的增大,似然分布变得更窄,表示观测数据更加集中,推断出的正确率更加有约束力。此时后验分布更偏向于似然。
3个 block的情况:总计进行了 385 次试次,其中有 231 次(60%)判断为正确
样本量进一步增大,似然分布更加集中,数据提供了更强的约束,推断出的正确率更加精确。此时后验分布更偏向于似然且分布形态随着似然的变窄而变窄。
结论
当似然反映的信息越集中时,它对后验的影响越大
样本量越大,似然对正确率\(\pi\)的约束力越强,后验分布也会更加集中于观测结果,这使得我们对\(\pi\)的推断更为确定。
Sequential analysis: Evolving with data#
在贝叶斯框架中,随着更多数据的到来,数据的影响力逐渐增加,先验信念的影响力逐渐减小,从而影响后验理解的演进,使得我们对正确率 \(\pi\) 的推断更为可靠。
随着数据的影响,后验如何演变?#
在随机点运动任务的例子中,我们逐步观察到随着样本量的增加:
先验信念的影响逐渐减弱:最初的先验分布提供了对正确率 \(\pi\) 的初步信念,但随着更多数据被观察到,先验对后验的影响逐渐减弱。
数据的主导地位逐渐增强:随着实验试次的增多,似然函数变得越来越窄,表示观测数据对正确率的推断更加集中和精确。
🤔思考时间:
数据对后验分布有着重要的影响。在实验当中,数据可能会分批次地进行输入,同时由于实验设计等因素的影响,数据输入顺序可能各不相同。那么,数据输入的先后顺序是否会影响后验分布的最终结果?
序列贝叶斯分析 (Sequential Bayesian Analysis)#
在以上例子中,随着被试的试次不断增加,后验分布也在逐步更新,更新过程如下:
更新步骤 |
Data (y, n) |
Model |
|---|---|---|
NA |
NA |
Beta(70, 30 ) = Beta(70, 30) |
a |
y = 77, n = 128 |
Beta(70 + 77, 30 + 128 - 77) = Beta(147, 81) |
a+b |
y = 152, n = 254 |
Beta(70 + 152, 30 + 254 - 152) = Beta(222, 132) |
a+b+c |
y = 231, n = 385 |
Beta(70 + 231, 30 + 385 - 231) = Beta(301, 184) |
思考:随着数据的更新,后验分布是如何变化的?
序列贝叶斯分析(又称贝叶斯学习)
在序列贝叶斯分析中,随着新数据的到来,后验模型会逐步更新。
每一份新数据都会使前一次后验模型(反映我们在观察到这些数据之前的理解)成为新的先验模型。

在序列贝叶斯分析当中,数据是分步(step)输入到模型当中的,随着数据的输入,后验分布也随之不断地更新。可以从两个视角来分析最终后验分布是否受到数据输入顺序的影响:
视角1:实例可视化
通过以下代码能够创建交互界面模拟贝叶斯学习过程:
import preliz as pz
import matplotlib.pyplot as plt
import numpy as np
import ipywidgets as widgets
import seaborn as sns
import pandas as pd
import warnings
# 忽略 FutureWarning
warnings.simplefilter(action='ignore', category=FutureWarning)
# 初始化计数器
count = -1
# 定义按钮点击时调用的函数
def on_button_clicked(b):
global count
count += 1
update_plot() # 调用更新函数
# 更新函数,它会重新执行 interactive_plot
def update_plot():
interactive_plot.update() # 更新 interactive_plot 的输出
# 创建按钮并绑定点击事件
button = widgets.Button(description="Update with more data", layout=widgets.Layout(width='400px', height='60px', border_radius='10px'))
# 设置按钮的背景颜色为蓝色,字体颜色为白色
button.style.button_color = '#1E90FF' # 浅蓝色 (可以调整为其他蓝色)
button.style.font_color = 'red' # 字体颜色为白色
button.on_click(on_button_clicked)
def plot_func(
data:pd.Series,
prior_alpha = 1,
prior_beta = 1,
init_trial = 20,
step=1,
show_prior = True,
show_last_post = True
):
"""
绘制贝叶斯更新过程中的后验分布和先验分布。
参数:
- data: pd.Series,包含每次试验的结果(0 或 1)。
- prior_alpha: float,beta分布的先验参数alpha。
- prior_beta: float,beta分布的先验参数beta。
- init_trial: int,初始试验的编号。
- step: int,每次更新的步长。
- show_prior: bool,是否显示先验分布。
- show_last_post: bool,是否显示上一次试验的后验分布。
返回:
- ax: 当前绘制的图表对象。
"""
# 使用全局变量`count`来记录当前试验轮次
global count
# 计算上一次试验和当前试验的编号
trial_number_last = init_trial + (count-1) * step
trial_number_current = init_trial + count * step
# 获取当前的绘图对象
ax = plt.gca()
# 定义x轴上从0到1的1000个点
x = np.linspace(0,1,1000)
# 如果show_prior为True,绘制先验分布
if show_prior:
y = pz.Beta(prior_alpha,prior_beta).pdf(x)
ax.plot(x,y, "-.", label="prior", color = "navy")
# 如果count小于0,只显示先验分布并退出
if count < 0:
ax.set_title(f"Prior Beta: alpha={prior_alpha}, beta={prior_beta}")
return ax
# 如果当前试验编号超出数据长度,显示所有试验的结果并退出
elif trial_number_current > data.shape[0]:
ax.set_title(f"All Trials {data.shape[0]} with {data.sum()} corrects")
return ax
# 如果count等于0,显示初始试验的结果
elif count == 0:
tmp_data = data[:trial_number_current]
ax.set_title(f"Trial {trial_number_current-init_trial} with {tmp_data.shape[0]} trials and {tmp_data.sum()} corrects")
# 如果count大于0,显示上一次试验的后验分布(如果需要)和当前试验结果
elif count > 0:
tmp_data = data[trial_number_last:trial_number_current]
ax.set_title(f"Trial {trial_number_last} with {tmp_data.shape[0]} trials and {tmp_data.sum()} corrects")
# 如果show_last_post为True,显示上一次试验的后验分布
if show_last_post:
n_correct = data[:trial_number_last].sum()
n_false = data[:trial_number_last].shape[0] - n_correct
post_alpha = prior_alpha + n_correct
post_beta = prior_beta + n_false
y = pz.Beta(post_alpha,post_beta).pdf(x)
ax.plot(x, y, label="posterior (t-1)", color = "olive", alpha = 0.3)
# 计算当前试验的后验分布并绘制
n_correct = data[:trial_number_current].sum()
n_false = data[:trial_number_current].shape[0] - n_correct
post_alpha = prior_alpha + n_correct
post_beta = prior_beta + n_false
# 绘制当前试验的后验分布
y = pz.Beta(post_alpha,post_beta).pdf(x)
ax.plot(x,y, label="posterior", color = "orangered")
# 显示图例并去除图框
ax.legend()
sns.despine()
# 使用 interactive 创建界面
interactive_plot = widgets.interactive(
plot_func,
data=widgets.fixed(data_subj1.correct),
prior_alpha=(1, 200, 1),
prior_beta=(1, 200, 1),
init_trial=(1, 100, 1),
step=(1, 20, 1)
)
# 显示按钮和 interactive 组件
display(button, interactive_plot)
可以通过调整inti_trial参数以及step参数改变数据输入顺序(或者点击update with moer data按钮),观察数据输入顺序对最终后验分布的影响。 通过交互式示例操作可得出——贝叶斯推断一个最大的特性就是能够随着新数据的加入而演进。这种序列分析还有两个基本且符合常识的特点:
序列不变性:后验分布不受数据输入的序列影响,只要数据总量相同,最终结果是一致的。
累积数据依赖性:我们可以逐步或一次性评估数据,后验分布只依赖于观测数据的总量。
特性1: 序列不变性#
在不同观测序列下的观测数据及对应的后验分布,尽管序列不同,最终结果将一致:
观测序列 |
Data (y, n) |
Model |
|---|---|---|
NA |
NA |
Beta(70, 30 ) = Beta(70, 30) |
a |
y = 77, n = 128 |
Beta(70 + 77, 30 + 128 - 77) = Beta(147, 81) |
a+b |
y = 152, n = 254 |
Beta(70 + 152, 30 + 254 - 152) = Beta(222, 132) |
a+b+c |
y = 231, n = 385 |
Beta(70 + 231, 30 + 385 - 231) = Beta(301, 184) |
为了更好地展示序列不变性,假设被试先从区块b开始进行实验,按照b、b+c和a+b+c的序列进行更新,更新的表格如下:
观测序列 |
Data (y, n) |
Model |
|---|---|---|
NA |
NA |
Beta(70, 30) = Beta(70, 30) |
b |
y = 75, n = 126 |
Beta(70 + 75, 30 + 126 - 75) = Beta(145, 81) |
b+c |
y = 154, n = 257 |
Beta(70 + 154, 30 + 257 - 154) = Beta(224, 133) |
a+b+c |
y = 231, n = 385 |
Beta(70 + 231, 30 + 385 - 231) = Beta(301, 184) |
无论采取哪种序列进行观测,最终的后验分布将基于总成功数和总试次数的合并计算。
特性2: 累积数据依赖性#
例如,在这三次的随机点运动任务中,共有 \(n = 128 + 254 + 385 = 767\) 次试次,其中 \(Y = 77 + 152 + 231 = 460\) 次判断正确。
初始先验分布是 \(\text{Beta}(70, 30)\),通过累积数据可以直接计算出后验分布为:
根据累积数据依赖性,后验分布只依赖于观测数据的总量,而不关心观测的序列,无论观测序列如何,最终的后验分布都为\(\text{Beta}(530, 337)\).
视角2:数学证明
在之前的讨论中,我们通过实例展示了数据序列不变性的特点。接下来,我们将为该特性在所有贝叶斯模型中的适用性进行数学证明。
数据序列不变性
定义 \(\theta\) 为感兴趣的任意参数,其先验概率密度函数为 \(f(\theta)\)。无论我们先观察数据点 \(y_1\) 然后观察 \(y_2\),还是先观察 \(y_2\) 再观察 \(y_1\),最终的后验分布都是相同的,即:
同样,无论我们一次性观察所有数据,还是按序列逐步观察数据,最终的后验分布都不受影响。
数学证明#
为了证明这一点,我们首先考虑通过序列观察数据 \(y_1\) 和 \(y_2\) 来构建的后验概率密度函数 \(f(\theta \mid y_1, y_2)\)。
在这个过程中,后验概率的演化可以分两步进行:
第一步:我们首先从原始先验分布 \(f(\theta)\) 和基于第一个数据点 \(y_1\) 的似然函数 \(L(\theta \mid y_1)\) 构建后验分布:
\[ f(\theta \mid y_1) = \frac{f(\theta) L(\theta \mid y_1)}{f(y_1)} \]其中,\(f(y_1)\) 是归一化常数,用于确保后验分布的积分为 1。
第二步:在观察到新的数据 \(y_2\) 后,我们使用 \(f(\theta \mid y_1)\) 作为先验,并根据数据 \(y_2\) 更新模型:
\[ f(\theta \mid y_2, y_1) = \frac{f(\theta \mid y_1) L(\theta \mid y_2)}{f(y_2)} \]代入第一步中的 \(f(\theta \mid y_1)\),得到:
\[ f(\theta \mid y_2, y_1) = \frac{\frac{f(\theta) L(\theta \mid y_1)}{f(y_1)} L(\theta \mid y_2)}{f(y_2)} \]化简后:
\[ f(\theta \mid y_2, y_1) = \frac{f(\theta) L(\theta \mid y_1) L(\theta \mid y_2)}{f(y_1) f(y_2)} \]
类似地,以相反的序列,先观察 \(y_2\) 然后观察 \(y_1\),我们得到同样的后验分布:
因此,后验分布 \(f(\theta \mid y_1, y_2)\) 与 \(f(\theta \mid y_2, y_1)\) 相同,证明了数据的序列不会影响最终的后验分布。
一次性观察数据 vs 序列观察数据#
不仅数据的序列不影响后验分布,观察数据的方式(一次性或逐步)也不影响最终结果。为此,假设我们从先验分布 \(f(\theta)\) 开始,并同时观察数据 \((y_1, y_2)\)。假设这些数据点在无条件和有条件下是独立的,那么:
因此,从同时观察数据 \((y_1, y_2)\) 得到的后验分布为:
代入条件独立性假设:
这与序列观察数据所得的后验分布相同:
因此,不论是一次性观察所有数据,还是按序列逐步观察数据,最终的后验分布是相同的。
总结:
贝叶斯序列分析的两大特性——数据序列不变性和累积数据依赖性——可以通过以上数学证明得到验证。
无论数据是序列观察还是一次性观察,或者数据序列如何变化,最终的后验分布总是不变的。
这一特性使得贝叶斯分析在处理动态和实时数据时具有极大的灵活性和可靠性。
